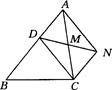
如图,在四边形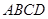 中,
中,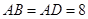 ,
,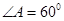 ,
,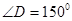 ,已知四边形的周长为32,求
,已知四边形的周长为32,求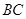 的长.
的长. 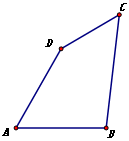
已知:关于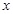 的一元二次方程
的一元二次方程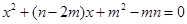 .
.
(1)求证:方程有两个实数根;
(2)若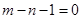 ,求证:方程有一个实数根为1.
,求证:方程有一个实数根为1.
在一次同学聚会中,每两名同学之间都互送了一件礼物,所有同学共送了90件礼物,共有多少名同学参加了这次聚会?
小明学完统计知识后,随机调查了他所住小区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图: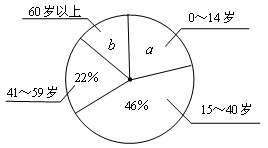
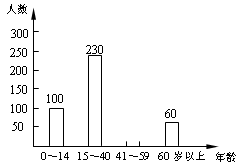
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小明共调查了名居民的年龄,扇形统计图中a=,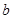 =;
=;
(2)补全条形统计图;
(3)若该辖区年龄在0~14岁的居民约有3500人,请估计年龄在15~59岁的居民的人数.
已知:如图,点 是
是 的边
的边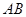 上一点,
上一点,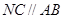 ,
, 交
交 于点
于点 ,若
,若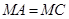 ,求证:
,求证: .
.