如图,矩形ABCD中,AB=6,BC=10,点P在边BC上,点Q在边CD上,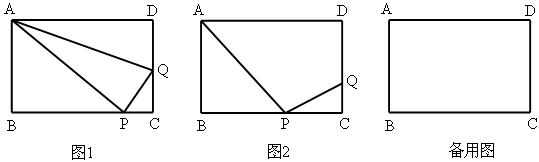
(1)如图1,将△ADQ沿AQ折叠,点D恰好与点P重合,求CQ的长;
(2)如图2,若CQ=2,且△ABP与△PCQ相似,求BP的长;
(3)若点Q是CD边上的一点,且BC上不存在满足AP⊥PQ的点P,请探究:此时CQ的长必须满足什么条件?
如图,已知直线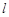 经过点A(1,0),与双曲线
经过点A(1,0),与双曲线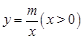 交于点B(2,1).过点P(
交于点B(2,1).过点P(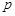 ,
,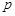 -1)(其中
-1)(其中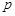 >1)作
>1)作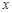 轴的平行线分别交双曲线
轴的平行线分别交双曲线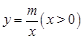 和
和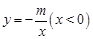 于点M、N.
于点M、N.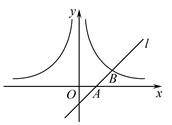
(1)求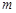 的值;
的值;
(2)求直线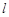 的解析式;
的解析式;
(3)是否存在实数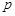 ,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的
,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的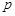 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水及提示计费价格表的部分信息:
| 自来水销售价格 |
污水处理价格 |
|
| 每户每月用水量 |
单价:元/吨 |
单价:元/吨 |
| 17吨以下 |
a |
0.80 |
| 超过17吨但不超过30吨的部分 |
b |
0.80 |
| 超过30吨的部分 |
6.00 |
0.80 |
(说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费用)
已知小王家2013年1月份用水20吨,交水费66元;2月份用水25吨,交水费91元.
(1)求a、b的值;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把6月份的水费控制在不超过家庭月收入的2%.若小王家的月收入为9200元,则小王家6月份最多能用水多少吨?
某校将举办“心怀感恩·孝敬父母”的活动,为此,校学生会就全校1 000名同学暑假期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成如下条形统计图.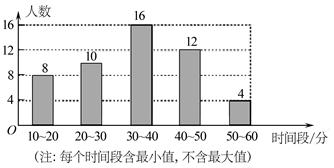
(1)本次调查抽取的人数为,估计全校同学在暑假期间平均每天做家务活的时间在40分钟以上(含40分钟)的人数为;
(2)校学生会拟在表现突出的甲、乙、丙、丁四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到甲、乙两名同学的概率.
用你发现的规律解答下列问题.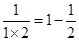 ;
;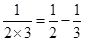 ;
;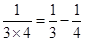 ;……
;……
(1)计算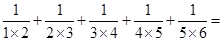 .
.
(2)探究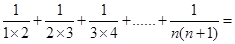 .(用含有
.(用含有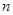 的式子表示)
的式子表示)
(3)若 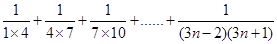 的值为
的值为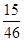 ,求
,求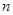 的值.
的值.
先化简分式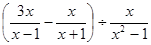 ,再从不等式组
,再从不等式组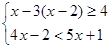 的解集中取一个合适的值代人,求原分式的值.
的解集中取一个合适的值代人,求原分式的值.