已知直线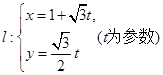 ,曲线
,曲线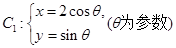 .
.
(1)设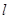 与
与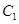 相交于
相交于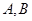 两点,求
两点,求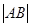 ;
;
(2)若把曲线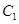 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的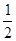 ,纵坐标压缩为原来的
,纵坐标压缩为原来的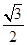 得到曲线
得到曲线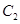 ,设点
,设点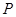 是曲线
是曲线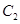 上的一个动点,求它到直线
上的一个动点,求它到直线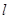 的距离的最大值.
的距离的最大值.
现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
(1)求该射手恰好命中一次的概率.
(2)求该射手的总得分X的分布列.
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.
(1)设该选手参赛的轮次为ξ,求ξ的分布列.
(2)对于(1)中的ξ,设“函数f(x)=3sin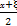 π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.
根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
| API |
0~50 |
51~ 100 |
101~ 150 |
151~ 200 |
201~ 250 |
251~ 300 |
>300 |
| 级 别 |
Ⅰ |
Ⅱ |
Ⅲ1 |
Ⅲ2 |
Ⅳ1 |
Ⅳ2 |
Ⅴ |
| 状 况 |
优 |
良 |
轻微 污染 |
轻度 污染 |
中度 污染 |
中度 重污染 |
重度 污染 |
 |
 |
 |
 |
 |
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.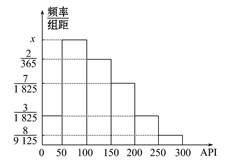
(1)求直方图中x的值.
(2)计算一年中空气质量分别为良和轻微污染的天数.
(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
(结果用分数表示.
已知57=78125,27=128,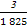 +
+ +
+ +
+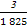 +
+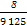 =
= ,365=73×5).
,365=73×5).
某校举行环保知识大奖赛,比赛分初赛和决赛两部分.初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题连续两次答错的概率为 .(已知甲回答每个问题的正确率相同,并且相互之间没有影响.)
.(已知甲回答每个问题的正确率相同,并且相互之间没有影响.)
(1)求选手甲回答一个问题的正确率.
(2)求选手甲可进入决赛的概率.
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率.
(2)求取出的4个球中恰有1个红球的概率.