如图所示，已知空间四边形
的每条边和对角线长都等于1，点
，
，
分别是
、
、
的中点，计算：
（1）
；
（2）
的长；
（3）异面直线
与
所成角的余弦值．
(本小题满分14分)
已知函数f(x)=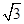 
sinxcosx－cos2x+
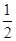(x∈R)．
(1)求函数f(x)的最小正周期；
(2)求函数f(x)在区间[0，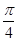
]上的值域．
设二次函数
满足：（1）
的解集是（0，1）；（2）对任意
都有
成立。数列
（I）求
的值；
（II）求的解析式；
（III）求证：
在直角坐标平面内y轴右侧的一动点P到点
的距离比它到y轴的距离大
（I）求动点P的轨迹C的方程；
（II）设Q为曲线C上的一个动点，点B，C在y轴上，若△QBC为圆
的外切三角形，求△QBC面积的最小值。
已知函数
（I）讨论
在其定义域上的单调性；
（II）当
时，若关于x的方程
恰有两个不等实根，求实数k的取值范围。
如图18图，已知AA1//BB1//CC1，且AA1=BB1=2CC1=2，AA1⊥面A1B1C1，△A1B1C1是边长为2的正三角形，M为BC的中点。
（1）求证：MA1⊥B1C1；
（2）求二面角C1—MB1—A1的平面角的正切值。