在三棱柱 中,已知
中,已知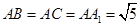 ,
, ,
,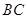 的中点为
的中点为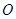 ,
,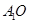 垂直于底面
垂直于底面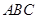 .
.
(1)证明:在侧棱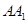 上存在一点
上存在一点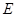 ,使得
,使得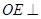 平面
平面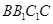 ,并求出
,并求出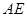 的长;
的长;
(2)求二面角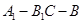 的平面角的余弦值.
的平面角的余弦值.
(本小题满分10分)
已知点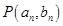 在函数
在函数 图象上,数列
图象上,数列 是以
是以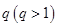 为公比的等比数列,
为公比的等比数列,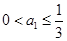 .
.
(Ⅰ)设 ,且
,且 ,求
,求 的值;
的值;
(Ⅱ)令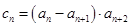 ,当
,当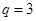 时,证明:
时,证明: .
.
(本小题满分12分)
给定正实数 ,对任意的正整数
,对任意的正整数 ,
, ,其中
,其中 表示不超过实数
表示不超过实数 的最大整数.
的最大整数.
(Ⅰ)若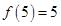 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)求证:(i)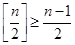 ;
;
(ii)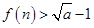 .
.
(本小题满分10分)
已知函数 其中
其中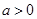 ,
, .
.
(Ⅰ)若 为奇函数,求
为奇函数,求 的值;
的值;
(Ⅱ)若 在
在 上单调递减,求
上单调递减,求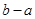 的值.
的值.
(本小题满分10分)
在△ 中,角
中,角 所对应的边分别为
所对应的边分别为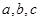 ,已知
,已知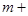

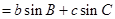
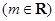 ,且
,且 .
.
(Ⅰ)当 ,且△
,且△ 的面积
的面积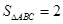 时,求边
时,求边 的值;
的值;
(Ⅱ)当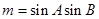 时,求角
时,求角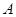 的值.
的值.
(本小题满分14分)
设抛物线 :
:
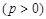 的焦点为
的焦点为 ,过
,过 且斜率为
且斜率为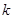 的直线
的直线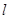 交抛物线
交抛物线 于
于 ,
, 两点,且
两点,且 .
.
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ)已知点 ,且
,且 的面积为
的面积为 ,求
,求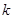 的值.
的值.