已知函数 是奇函数.
是奇函数.
(1)求实数m的值;
(2)是否存在实数 ,当
,当 时,函数
时,函数 的值域是
的值域是 .若存在,求出实数
.若存在,求出实数 ;若不存在,说明理由;
;若不存在,说明理由;
(3)令函数 ,当
,当 时,求函数
时,求函数 的最大值.
的最大值.
(满分12分)已知圆O: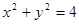 ,点P在直线
,点P在直线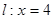 上的动点。
上的动点。
(1)若从P到圆O的切线长为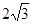 ,求P点的坐标以及两条切线所夹劣弧长;
,求P点的坐标以及两条切线所夹劣弧长;
(2)若点A(-2,0),B(2,0),直线PA,PB与圆O的另一个交点分别为M,N,求证:直线MN经过定点(1,0)。
(满分12分)定义在R上的奇函数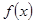 有最小正周期4,且
有最小正周期4,且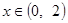 时,
时,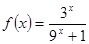 。
。
(1)求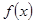 在
在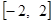 上的解析式;
上的解析式;
(2)判断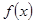 在(0,2)上的单调性,并给予证明;
在(0,2)上的单调性,并给予证明;
(3)当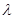 为何值时,关于方程
为何值时,关于方程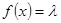 在
在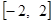 上有实数解?
上有实数解?
(满分12分) 是等差数列
是等差数列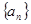 的前
的前 项和,
项和, ,
, 。
。
(1)求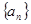 的通项公式;
的通项公式;
(2)设 (
(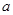 是实常数,且
是实常数,且 ),求
),求 的前
的前 项和
项和 。
。
(满分12分)设命题P:关于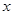 的不等式:
的不等式: 的解集是R,命题Q:函数
的解集是R,命题Q:函数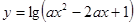 的定义域为R,若P或Q为真,P且Q为假,求
的定义域为R,若P或Q为真,P且Q为假,求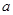 的取值范围。
的取值范围。
(满分10分)已知函数
(1)求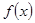 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)求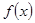 在区间
在区间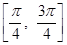 上的取值范围。
上的取值范围。