如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使它与△ABC全等且A与A1是对应点;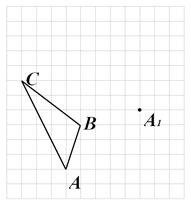
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.

图中的不明飞行物是将坐标(0,0),(1,0),(3,0),(2,1),(3,4),(5,3),(5,2),(3,2)的点用线段依次连接而成的.
下面将以上各点做如下变化:
(1)横坐标保持不变,纵坐标分别乘以-1,所得图案与原图案有什么变化?
(2)横坐标和纵坐标都乘以-1,所得图案与原图案相比有什么变化?
(3)横坐标加1,纵坐标加2,所得图案与原图案相比有什么变化?
如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°.求∠D的度数.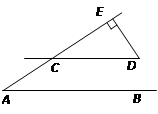
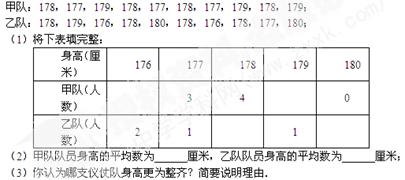
依法纳税是每个公民应尽的义务.从2008年3月1日起,新修改后的《中华人民共和国个人所得税法》规定,公民每月收入不超过2000元,不需交税;超过2000元的部分为全月应纳税所得额,都应纳税,且根据超过部分的多少按不同的税率纳税,详细的税率如下表:
| 级别 |
全月应纳税所得额 |
税率(%) |
| 1 |
不超过500元的部分 |
5 |
| 2 |
超过500元至2 000元的部分 |
10 |
| 3 |
超过2 000元至5 000元的部分 |
15 |
| 4 |
超过5 000元至20 000元的部分 |
20 |
| … |
… |
… |
(1)某工厂一名工人2008年3月的收入为2 400元,问他应交税款多少元?
(2)设x表示公民每月收入(单位:元),y表示应交税款(单位:元),
当2500≤x≤4000时,请写出y关于x的函数关系式;
(3)某公司一名职员2008年4月应交税款120元,问该月他的收入是多少元?