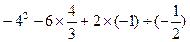(本题8分)
学校“环保小组”的同学以60米/分的速度从学校出发,步行到距学校1000米的文化广场宣传环保知识. 5分钟后,小明以110米/分的速度从学校出发追赶“环保小组”,并且在途中追上了他们.求:
(1)小明用了多长时间追上“环保小组”?
(2)当小明追上“环保小组”时距离文化广场还有多远?
(本题7分)
今年元旦节里,小明全家外出旅游,共用了8600元. 回来后小明把费用支出情况制成了如下的统计图,请根据图上的信息解答下列问题:
(1)图中哪一部分的费用占全部费用的 ?
?
(2)他们在食宿方面用了多少元?
(3)他们的交通费共支出了多少元?
(本题7分)解方程: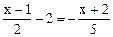
(本题6分)
先化简,再求值: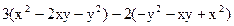 ,其中
,其中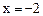 ,
,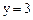
(本题6分)计算: