已知抛物线 的方程为
的方程为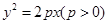 ,点
,点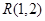 在抛物线
在抛物线 上.
上.
(1)求抛物线 的方程;
的方程;
(2)过点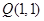 作直线交抛物线
作直线交抛物线 于不同于
于不同于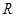 的两点
的两点 ,
,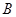 ,若直线
,若直线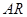 ,
,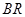 分别交直线
分别交直线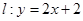 于
于 ,
, 两点,求
两点,求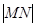 最小时直线
最小时直线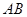 的方程.
的方程.
(本小题满分14分)
如图5,在三棱柱 中,侧棱
中,侧棱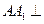 底面
底面 ,
,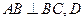 为
为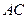 的中点,
的中点, ,
,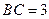 .
.
(1)求证: 平面
平面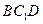 ;
;
(2) 求四棱锥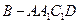 的体积.
的体积. 图5
图5
(本小题满分12分)
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重
量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图4.
(1)根据样品数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过2克的概率.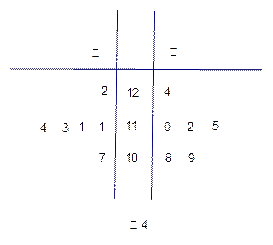
(本小题满分12分)已知函数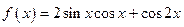 (
(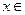 R).
R).
(1)求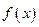 的最小正周期和最大值;
的最小正周期和最大值;
(2)若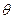 为锐角,且
为锐角,且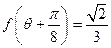 ,求
,求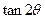 的值.
的值.
(本小题满分14分)
已知集合 是满足下列性质的函数
是满足下列性质的函数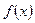 的全体:在定义域内存在
的全体:在定义域内存在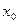 ,使得
,使得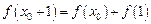 成立。
成立。
(Ⅰ)函数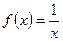 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(Ⅱ)设函数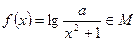 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设函数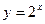 图象与函数
图象与函数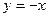 的图象有交点,证明:函数
的图象有交点,证明:函数 .
.
(本小题满分14分)
建造一容积为8 深为2m的长方体形无盖水池,每
深为2m的长方体形无盖水池,每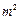 池底和池壁造价各为120元和80元.
池底和池壁造价各为120元和80元.
(1)求总造价关于一边长x的函数解析式,并指出该函数的定义域;
(2)判断(1)中函数在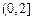 和
和 上的单调性;
上的单调性;
(3)如何设计水池尺寸,才能使总造价最低;