已知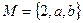 ,
,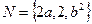 ,且
,且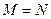 ,求
,求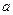 ,
,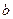 的值
的值
(本小题12分)
已知 是等差数列,且
是等差数列,且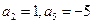
①求 的通项
的通项 。
。
②求 的前n项和Sn的最大值。
的前n项和Sn的最大值。
(本小题12分)
一海轮以20海里/小时的速度向正东航行,它在A点时测得灯塔P在船的北偏东60°方向上,2小时后船到达B点时测得灯塔P在船的北偏东45°方向上。求:
①船在B点时与灯塔P的距离。
②已知以点P为圆心,55海里为半径的圆形水城内有暗礁,那么这船继续向正东航行,有无触礁的危险?
(本小题满分14分)对于定义在区间D上的函数 ,若存在闭区间
,若存在闭区间 和常数
和常数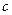 ,使得对任意
,使得对任意 ,都有
,都有 ,且对任意
,且对任意 ∈D,当
∈D,当 时,
时,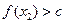 恒成立,则称函数
恒成立,则称函数 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数 和
和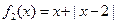 是否为R上的“平底型”函数?并说明理由;
是否为R上的“平底型”函数?并说明理由;
(Ⅱ)设 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式 对一切
对一切 R恒成立,求实数
R恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数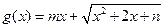 是区间
是区间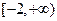 上的“平底型”函数,求
上的“平底型”函数,求 和
和 的值.
的值.
(本小题满分14分)已知线段 ,
, 的中点为
的中点为 ,动点
,动点 满足
满足 (
( 为正常数).
为正常数).
(Ⅰ)建立适当的直角坐标系,求动点 所在的曲线方程;
所在的曲线方程;
(Ⅱ)若 ,动点
,动点 满足
满足 ,且
,且 ,试求
,试求 面积的最大值和最小值.
面积的最大值和最小值.
某研究小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试的成绩(百分制)如下表所示:
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
| 物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
80 |
| 序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 数学成绩 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
84 |
72 |
83 |
| 物理成绩 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
82 |
78 |
86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85分(含85分)以上为优秀。
⑴根据上表完成下面的 列联表:
列联表:
| 数学成绩优秀 |
数学成绩不优秀 |
合计 |
|
| 物理成绩优秀 |
|||
| 物理成绩不优秀 |
12 |
||
| 合计 |
20 |
⑵根据⑴中表格的数据计算,有多少的把握,认为学生的数学成绩与物理成绩之间有关系?