【2015高考安徽,理21】设函数 .
.
(Ⅰ)讨论函数 在
在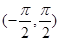 内的单调性并判断有无极值,有极值时求出极值;
内的单调性并判断有无极值,有极值时求出极值;
(Ⅱ)记 ,求函数
,求函数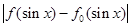 在
在 上的最大值D;
上的最大值D;
(Ⅲ)在(Ⅱ)中,取 ,求
,求 满足
满足 时的最大值.
时的最大值.
已知复数z1=m(m-1)+(m-1)i是纯虚数.
(1)求实数m的值;
(2)若(3+z1) =4+2i,求复数z.
=4+2i,求复数z.
某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?
在数列 中,
中, ,且满足
,且满足
 .
.
(Ⅰ)求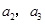 及数列
及数列 的通项公式;
的通项公式;
(Ⅱ)设 求数列
求数列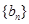 的前
的前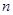 项和
项和 .
.
如图是一个直三棱柱(以A1B1C1为底面)被一平面
所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,
AAl=4,BBl=2,CCl=3,且设点O是AB的中点。
(1)证明:OC∥平面A1B1C1;
(2)求异面直线OC与AlBl所成角的正切值。
已知数列 满足
满足 ,则(1)当
,则(1)当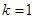 时,求数列
时,求数列 的前
的前 项和
项和 ;(2)当
;(2)当 时,证明数列
时,证明数列 是等比数列。
是等比数列。