【2015江苏高考，17】（本小题满分14分）某山区外围有两条相互垂直的直线型公路，为进一步改善山区的交通现状，计划修建一条连接两条公路的山区边界的直线型公路，记两条相互垂直的公路为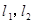
，山区边界曲线为C，计划修建的公路为l，如图所示，M，N为C的两个端点，测得点M到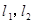的距离分别为5千米和40千米，点N到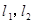的距离分别为20千米和2．5千米，以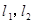所在的直线分别为x，y轴，建立平面直角坐标系xOy，假设曲线C符合函数
（其中a，b为常数）模型．
（1）求a，b的值；
（2）设公路l与曲线C相切于P点，P的横坐标为t．
①请写出公路l长度的函数解析式
，并写出其定义域；
②当t为何值时，公路l的长度最短？求出最短长度．
，其中
，求
在
上的最值；
的取值范围；
时，令
，试证：
恒成立.
，并且经过点
.
的直线
经过点
，且与椭圆交于不同的两点
,求
面积的最大值.
中，底面
是边长为2的菱形，
E、F分别是PB、CD的中点，且
.
；
;
的余弦值.
满足
的值；
，使得数列
为等差数列，请说明理由.
中，角
、B、C的对边分别为a，b，c，且
，
的值；
的值.