设函数 ,其中
,其中
(1)若 ,求
,求 在
在 上的最值;
上的最值;
(2)若 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围;
(3)当 时,令
时,令 ,试证:
,试证: 恒成立.
恒成立.
(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—5:不等式选讲
设函数 .
.
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若不等式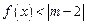 的解集是非空的集合,求实数
的解集是非空的集合,求实数 的取值范围.
的取值范围.
(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的 轴的正半轴重合.直线
轴的正半轴重合.直线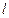 的参数方程是
的参数方程是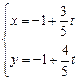 (
( 为参数),曲线
为参数),曲线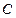 的极坐标方程为
的极坐标方程为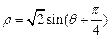 .
.
(Ⅰ)求曲线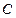 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线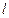 与曲线
与曲线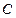 相交于
相交于 ,
,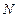 两点,求M,N两点间的距离.
两点,求M,N两点间的距离.
(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—1:几何证明选讲
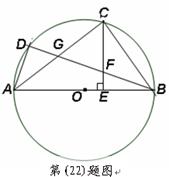
如图,已知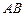 是
是 的直径,
的直径, ,
,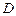 是
是 上两点,
上两点, 于
于 ,
,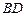 交
交 于
于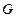 ,交
,交 于
于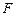 ,
, .
.
(Ⅰ)求证: 是
是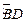 的中点;
的中点;
(Ⅱ)求证: .
.
(本小题满分 分)已知函数
分)已知函数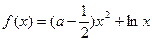 (
( ).
).
(Ⅰ)当 时,求
时,求 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数 的图象恒在直线
的图象恒在直线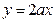 下方,求
下方,求 的取值范围.
的取值范围.
(本小题满分 分)在平面直角坐标系中,已知两个定点
分)在平面直角坐标系中,已知两个定点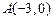 和
和 .动点
.动点 在
在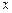 轴上的射影是
轴上的射影是 (
( 随
随 移动而移动),若对于每个动点M总存在相应的点
移动而移动),若对于每个动点M总存在相应的点 满足
满足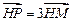 ,且
,且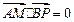 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设过定点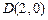 的直线
的直线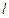 (直线
(直线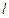 与
与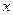 轴不重合)交曲线
轴不重合)交曲线 于
于 ,
,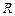 两点,求证:直线
两点,求证:直线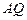 与直线
与直线 交点总在某直线
交点总在某直线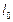 上.
上.