已知椭圆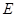 的中心在坐标原点
的中心在坐标原点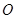 ,焦点在坐标轴上,且经过
,焦点在坐标轴上,且经过 两点.
两点.
(1)求椭圆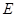 的方程;
的方程;
(2)已知定点 ,
,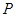 点为椭圆上的动点,求
点为椭圆上的动点,求 最大值及相应的
最大值及相应的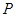 点坐标.
点坐标.
如图,在直三棱柱 中,
中, ,
, ,
, ,点
,点 分别在棱
分别在棱 上,且
上,且 .
.
(1)求三棱锥 的体积;
的体积;
(2)求异面直线 与
与 所成的角的大小.
所成的角的大小.
设条件 :实数
:实数 满足
满足 ;条件
;条件 :实数
:实数 满足
满足 且命题“若
且命题“若 ,则
,则 ”的逆否命题为真命题,求实数
”的逆否命题为真命题,求实数 的取值范围.
的取值范围.
在平面直角坐标系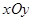 中,与向量
中,与向量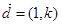 平行的直线
平行的直线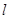 经过椭圆
经过椭圆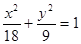 的右焦点
的右焦点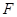 ,与椭圆相交于
,与椭圆相交于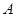 、
、 两点.
两点.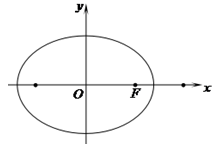
(1)若点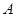 在
在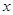 轴的上方,且
轴的上方,且 ,求直线
,求直线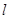 的方程;
的方程;
(2)若 ,
,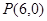 ,求△
,求△ 的面积;
的面积;
(3)当 (
(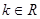 且
且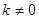 )变化时,是否存在一点
)变化时,是否存在一点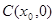 ,使得直线
,使得直线 和
和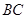 的斜率之和为
的斜率之和为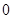 .若存在,请证明结论;若不存在,请说明理由.
.若存在,请证明结论;若不存在,请说明理由.
已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点.
(1)若|AB|= ,求|MQ|、Q点的坐标以及直线MQ的方程;
,求|MQ|、Q点的坐标以及直线MQ的方程;
(2)求证:直线AB恒过定点.