已知椭圆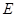 的中心在坐标原点
的中心在坐标原点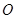 ,焦点在坐标轴上,且经过
,焦点在坐标轴上,且经过 两点.
两点.
(1)求椭圆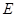 的方程;
的方程;
(2)已知定点 ,
,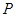 点为椭圆上的动点,求
点为椭圆上的动点,求 最大值及相应的
最大值及相应的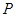 点坐标.
点坐标.
(本小题满分12分)
已知向量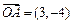 ,
, ,
,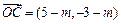 .
.
(Ⅰ)若点A、B、C能构成三角形,求实数m的取值范围;
(Ⅱ)若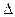 ABC为直角三角形,且
ABC为直角三角形,且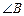 为直角,求实数m的值.
为直角,求实数m的值.
已知双曲线 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为 .过
.过
 的直线
的直线 与双曲线C交于不同的两点
与双曲线C交于不同的两点 、
、 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)当 时,求直线
时,求直线 的方程;
的方程;
(Ⅲ)设 (
( 为坐标原点),求
为坐标原点),求 的取值范围.
的取值范围.
已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),……(x n,y n),…
(Ⅰ)若程序运行中输出的一个数组是( , t),则t ="" ;
, t),则t ="" ;
(Ⅱ)程序结束时,共输出(x , y )的组数为;
(Ⅲ)写出流程图的程序语句.
已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
(Ⅰ)求正三棱柱的侧棱长.
(Ⅱ)若M为BC1的中点,试用基底向量 、
、 、
、 表示向量
表示向量 ;
;
(Ⅲ)求异面直线AB1与BC所成角的余弦值.
已知 ;¬
;¬ 是¬
是¬ 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.