关于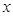
的方程
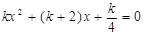有两个不相等的实数根．
（1）求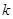
的取值范围．
（2）是否存在实数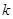，使方程的两个实数根的倒数和等于0?若存在，求出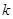的值；若不存在，说明理由．
已知A（0，－6），B（－3，0），C（m，2）三点在同一直线上，试求出图象经过其中一点的反比例函数的解析式，并在图中画出其图象．（要求标出必要的点，可不写画法）
已知：y＝y1＋y2，y1与x2成正比例，y2与x成反比例，且x＝1时，y＝3；x＝－1时，y＝1．求
时，y的值．
已知y是x的反比例函数，且x＝2时，y＝－3，确定此函数的解析式，并求当y＝－8时，自变量x的值．
已知：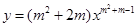
．
（1）当m为何值时，y是x的正比例函数？
（2）当m为何值时，y是x的二次函数？
（3）当m为何值时，y是x的反比例函数？
如图所示，在□ABCD中，点E，F分别为BC边上的点，且BE＝CF，AF＝DE求证：□ABCD是矩形．