(·辽宁营口)某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的 倍,且每天包装大黄米和江米的质量之和为45千克.
倍,且每天包装大黄米和江米的质量之和为45千克.
(1)求平均每天包装大黄米和江米的质量各是多少千克?
(2)为迎接今年6月20日的“端午节”,该超市决定在节日前20天增加每天包装大黄米和江米的质量,二者的包装质量与天数的变化情况如图所示,节日后又恢复到原来每天的包装质量.分别求出在这20天内每天包装大黄米和江米的质量随天数变化的函数关系式,并写出自变量的取值范围.
(3)假设该超市每天都会将当天包装后的大黄米和江米全部出售,已知大黄米成本价为每千克7.9元,江米成本价为每千克9.5元,二者包装费用平均每千克均为0.5元,大黄米售价为每千克10元,江米售价为每千克12元,那么在这20天中有哪几天销售大黄米和江米的利润之和大于120元? [总利润=售价额-成本-包装费用]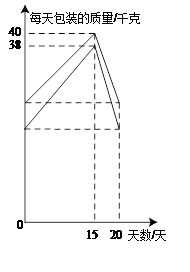
(·黑龙江省黑河市、齐齐哈尔市、大兴安岭)【10分】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足 ,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.
,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.
(1)求线段AB的长;
(2)求直线CE的解析式;
(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(·黑龙江省黑河市、齐齐哈尔市、大兴安岭)【8分】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.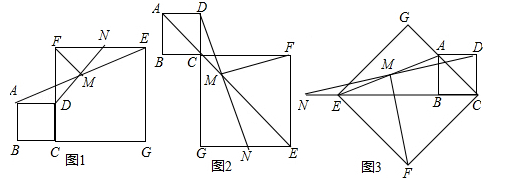
(·黑龙江哈尔滨)(本题10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+1(k≠0)与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2-(6a-2)x+b (a≠0)与直线AC交于另一点B,点B坐标为(4,3).
(1)求a的值;
(2)点p是射线CB上的一个动点,过点P在作PQ⊥x轴,垂足为点Q,在x轴上点Q的右侧取点M,使MQ= ,在QP的延长线上取点N,连接PM,AN,已知tan∠NAQ-tan∠MPQ=
,在QP的延长线上取点N,连接PM,AN,已知tan∠NAQ-tan∠MPQ= ,求线段PN的长;
,求线段PN的长;
(3)在(2)的条件下,过点C作CD⊥AB,使点D在直线AB 下方,且CD=AC,连接PD,NC,当以PN,PD,NC的长为三边长构成的三角形面积是 时,在y轴左侧的抛物线上是否存在点E,连接NE,PE,使得ΔENP与以PN、PD、NC的长为三边长的三角形全等?若存在,求出点E坐标;若不存在,请说明理由.
时,在y轴左侧的抛物线上是否存在点E,连接NE,PE,使得ΔENP与以PN、PD、NC的长为三边长的三角形全等?若存在,求出点E坐标;若不存在,请说明理由.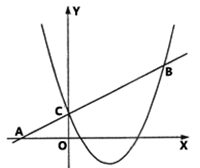
(·辽宁葫芦岛)如图,直线 与x轴交于点C,与y轴交于点B,抛物线
与x轴交于点C,与y轴交于点B,抛物线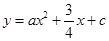 经过B、C两点.
经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.