某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
+6 |
-2 |
-4 |
+12 |
-10 |
+16 |
-8 |
(1)根据记录的数据可知该厂星期四生产自行车 辆;
(2)产量最多的一天比产量最少的一天多生产自行车 辆;
(3)根据记录的数据可知该厂本周实际生产自行车 辆;
(4)该厂实行每周计件工资制,每生产一辆车可得50元,若超额完成任务,则超过部分每辆另奖20元;少生产一辆扣25元,那么该厂工人这一周的工资总额是多少元?
解方程: .
.
先化简,再求值:(2a+1)2﹣2(2a+1)+3,其中a= .
.
我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段 为直径的圆.
为直径的圆.
(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
(3)某地有四个村庄 (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的 ,
, 处,直角边
处,直角边 在
在 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至 处时,设
处时,设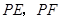 与
与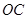 分别交于点
分别交于点 ,与
,与 轴分别交于点
轴分别交于点 .
.
(1)求直线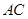 所对应的函数关系式;
所对应的函数关系式;
(2)当点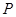 是线段
是线段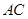 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:
①点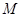 到
到 轴的距离
轴的距离 与线段
与线段 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及 取最大值时点
取最大值时点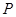 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.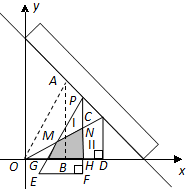
“爱心”帐篷集团的总厂和分厂分别位于甲、乙两市,两厂原来每周生产帐篷共9千顶,现某地震灾区急需帐篷14千顶,该集团决定在一周内赶制出这批帐篷.为此,全体职工加班加点,总厂和分厂一周内制作的帐篷数分别达到了原来的1.6倍、1.5倍,恰好按时完成了这项任务.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的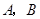 两地,由于两市通住
两地,由于两市通住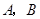 两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
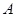 地 地 |
 地 地 |
||
| 每千顶帐篷 所需车辆数 |
甲市 |
4 |
7 |
| 乙市 |
3 |
5 |
|
| 所急需帐篷数(单位:千顶) |
9 |
5 |
请设计一种运送方案,使所需的车辆总数最少.说明理由,并求出最少车辆总数.