“爱心”帐篷集团的总厂和分厂分别位于甲、乙两市,两厂原来每周生产帐篷共9千顶,现某地震灾区急需帐篷14千顶,该集团决定在一周内赶制出这批帐篷.为此,全体职工加班加点,总厂和分厂一周内制作的帐篷数分别达到了原来的1.6倍、1.5倍,恰好按时完成了这项任务.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的 两地,由于两市通住
两地,由于两市通住 两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
| |
 地 地 |
 地 地 |
|
| 每千顶帐篷 所需车辆数 |
甲市 |
4 |
7 |
| 乙市 |
3 |
5 |
|
| 所急需帐篷数(单位:千顶) |
9 |
5 |
请设计一种运送方案,使所需的车辆总数最少.说明理由,并求出最少车辆总数.
已知关于x的方程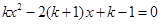 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
已知:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在BC上运动,点P不与点B,C重合,设PC=x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围.
某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30 20 21 20 26 30 25 21 19 28 26
(1)上述数据中,众数是__________万元,中位数是__________万元,平均数是__________万元;
(2)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
(每题4分,共12分)用你喜欢的方法解下列方程:
(1)
(2)
(3)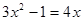
如图,在平面直角坐标系中,点A为二次函数y=-x2+4x-1图象的顶点,图象与y轴交于点C,过点A并与AC垂直的直线记为BD,点B,D分别为直线与y轴和x轴的交点,点E是二次函数图象上与点C关于对称轴对称的点,将一块三角板的直角顶点放在A点,绕点A旋转,三角板的两直角边分别与线段OD和线段OB相交于点P,Q两点.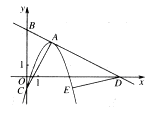
(1)点A的坐标为____,点c的坐标为____;
(2)求直线BD的表达式;
(3)在三角板旋转过程中,平面上是否存在点Q,使得以D,E,P,R为顶点的四边形为菱形?若存在,直接写出P,Q,R的坐标;若不存在,请说明理由.