如图，在平面直角坐标系中，点A为二次函数y=-x2+4x-1图象的顶点，图象与y轴交于点C，过点A并与AC垂直的直线记为BD，点B，D分别为直线与y轴和x轴的交点，点E是二次函数图象上与点C关于对称轴对称的点，将一块三角板的直角顶点放在A点，绕点A旋转，三角板的两直角边分别与线段OD和线段OB相交于点P，Q两点．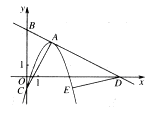
（1）点A的坐标为____，点c的坐标为____；
（2）求直线BD的表达式；
（3）在三角板旋转过程中，平面上是否存在点Q，使得以D，E，P，R为顶点的四边形为菱形?若存在，直接写出P，Q，R的坐标；若不存在，请说明理由．
已知x-1=
，求代数式（x+1）2-4（x+1）+4
解下列不等式（组）：
（1）解不等式
≤5－x；
（2）解不等式组：
．
如图，某公司组织员工假期去旅游，租用了一辆耗油量为每百公里约为25L的大巴车，大巴车出发前油箱有油100L，大巴车的平均速度为80km/h，行驶若干小时后，由于害怕油箱中的油不够，在途中加了一次油，油箱中剩余油量y（L）与行驶时间x（h）之间的关系如图所示，请根据图像回答下列问题：
（1）汽车行驶__________h后加油，中途加油__________L；
（2）求加油前油箱剩余油量y与行驶时间x的函数解析式；
（3）若当油箱中剩余油量为10L时，油量表报警，提示需要加油，大巴车不再继续行驶，则该车最远能跑多远？此时，大巴车从出发到现在已经跑了多长时间？
如图，在矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD，BC于点E，F，垂足为点O．
（1）连接AF，CE，求证：四边形AFCE为菱形。
（2）求菱形AFCE的边长
如图，在△ABC中，MN∥BD交AC于点P，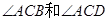 
的平分线分别交MN于点E，F。
（1）求证：PE=PF
（2）当MN与AC的交点P在什么位置时，四边形AECF是矩形，请说明理由；
（3）当△ABC满足什么条件时，四边形AECF是正方形（不需证明）