已知函数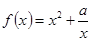 (
(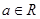 ).
).
(1)判断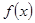 的奇偶性;
的奇偶性;
(2)当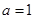 时,求证:函数
时,求证:函数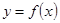 在区间
在区间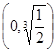 上是单调递减函数,在区间
上是单调递减函数,在区间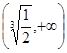 上是单调递增函数;
上是单调递增函数;
(3)若正实数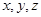 满足
满足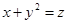 ,
,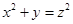 ,求
,求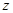 的最小值.
的最小值.
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为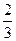 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为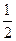 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概 率;
率;
(Ⅱ)在这项考试过程中,假设他不放 弃所有的考试机会,记他参加考试的次数为
弃所有的考试机会,记他参加考试的次数为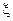 ,求
,求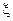 的数学期望E
的数学期望E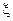 .
.
已知函数
(Ⅰ)求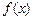 的最小正周期;
的最小正周期;
(Ⅱ)求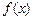 的单调增区间;
的单调增区间;
(Ⅲ)若 ,求
,求 的值.
的值.
已知函数 ,设
,设 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以 )图象上任意一点
)图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒
恒
成立,求实数 的最小值。
的最小值。
(Ⅲ)是否存在实数 ,使得函数
,使得函数 的图象与
的图象与 的图象恰
的图象恰
好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由。来
的取值范围,若不存在,说明理由。来
等比数列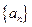 的各项均为正数,且
的各项均为正数,且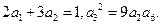
(1)求数列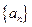 的通项公式.
的通项公式.
(2)设 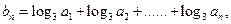 求数列
求数列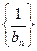 的前项和
的前项和
在 ABC中,内角A,B,C的对边分别为a,b,c.
ABC中,内角A,B,C的对边分别为a,b,c.
已知.
(1)求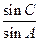 的值;
的值;
(2)若cosB=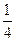 ,b=2,
,b=2, 的面积S。
的面积S。