如图，已知四棱锥P－ABCD的底面是直角梯形，∠ABC＝∠BCD＝90°，AB＝BC＝PB＝PC＝2CD＝2，侧面PBC⊥底面ABCD，点M在AB上，且
，E为PB的中点．
（1）求证：CE∥平面ADP；
（2）求证：平面PAD⊥平面PAB；
（3）棱AP上是否存在一点N，使得平面DMN⊥平面ABCD，若存在，求出
的值；若不存在，请说明理由．
（本小题共13分）设
，已知函数
.
（1）当
时，求函数
的单调区间；
（2）若对任意的
，有
恒成立，求实数
的取值范围.
（本小题共14分）如图，将矩形ABCD沿对角线BD把△ABD折起，使A点移到
点，且在平面BCD上的射影O恰好在CD上.
（1）求证：BC⊥
；
（2）求证：平面
⊥平面
；
（3）若AB=10，BC=6，求三棱锥
的体积.
（本小题共13分）在△ABC中，
分别是角
的对边，满足
，且
.
（1）求C的大小；
（2）求
的最大值，并求取得最大值时角A，B的值.
（本小题共13分）设数列
的前
项和为
，且
.
（1）求数列的通项公式；
（2）若数列
满足
，求数列的通项公式.
（本小题满分14分）给定正奇数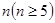
，数列
：
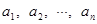是1，2，…，
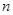的一个排列，定义E（
，…，
）
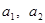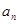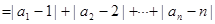为数列：
，
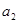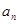，…，的位差和.
（1）当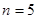
时，求数列：1，3，4，2，5的位差和；
（2）若位差和E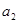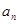（，，…，）=4，求满足条件的数列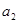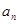：，，…，的个数；
（3）若位差和
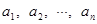，求满足条件的数列：的个数.