学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法,尝试用你积累的经验和方法解决下面问题.
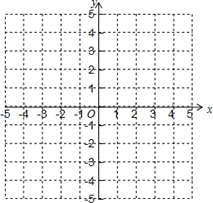
(1)在平面直角坐标系中,画出函数y=|x|的图象:
①列表:完成表格
| x |
… |
﹣3 |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
… |
| y |
… |
|
|
|
|
|
|
|
|
②画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|两条不同类型的性质;
(3)直接写出函数y=|x﹣2|图象是由函数y=|x|图象怎样平移得到?
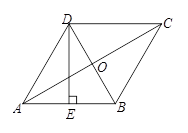
(本小题满分14分)如图,在菱形  中,
中, 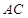 ,
, 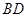 相交于点
相交于点 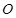 ,
, 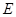 为
为  的中点,
的中点, 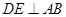 .
. 
(1)求 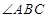 的度数;
的度数;
(2)如果 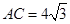 ,求
,求  的长.
的长.
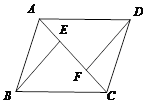
(本小题满分10分)已知:如图, 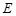 ,
, 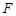 是□ABCD的对角线
是□ABCD的对角线 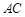 上的两点,
上的两点, 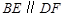 ,求证:
,求证: 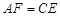 .
. 
小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为 、
、 、
、 ,求△ABC的面积.
,求△ABC的面积.
小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答:
(1)求图1中△ABC的面积;
参考小明解决问题的方法,完成下列问题:
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).
①利用构图法在答题卡的图2中画出三边长分别为 、
、 、
、 的格点△DEF;
的格点△DEF;
②计算△DEF的面积是 .
(3)如图3,已知△PQR,以PQ,PR为边向外作正方形PQAF,PRDE,连接EF.若PQ= ,PR=
,PR= ,QR=
,QR= ,求六边形AQRDEF的面积.
,求六边形AQRDEF的面积.
已知a,b,c满足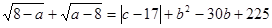 ,
,
(1)求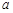 ,b,c的值;
,b,c的值;
(2)试问以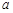 ,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长和面积;若不能构成三角形,请说明理由.
,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长和面积;若不能构成三角形,请说明理由.
如图,△AOB、△COD是等腰直角三角形,点D在AB上.
(1)求证:△AOC≌△BOD;
(2)若AD=3,BD=1,求CD和△ABC的面积.