如图1,已知锐角△ABC中,CD.BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.

(1)连接DM,ME,猜想∠A与∠DME之间的关系,并写出推理过程;
(2)求证:MN⊥DE;
(3)若将锐角△ABC变为钝角△ABC,如图2,上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,请说明理由.
地球赤道的周长约为40000㎞,我国13亿人手拉手能否绕地球赤道一周?
生活在地球上的人类非常需要绿色环境,若平均每人需要2.5m2的绿地,则100万人中的中等城市,规划时要安排多少绿化面积?
图中是某报社“百姓热线”一周内接到热线电话的统计图, 其中有关环境保护问题的电话最多,共70个,请回答下列问题.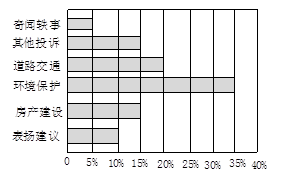
(1)本周“百姓热线”共接热线电话多少个?
(2)有关道路交通问题的电话有多少个?
下表是反映某地区某一天气温随时间变化的情况.
| 时间(时) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
| 温度℃ |
2 |
0 |
-2 |
0 |
3 |
5 |
8 |
10 |
9 |
8 |
7 |
5 |
3 |
请根据上面数据制成折线统计图, 并根据折线图大致描述一下该日该地区的气温大致变化.
下表是新中国成立以来历次人口普查中的部分数据.
| 全国人口总数(亿) |
文盲人口总数(亿) |
文盲比例(%) |
成人文盲率(%) |
|
| 1949年 |
3.6 |
2.9 |
80 |
|
| 1964年 |
6.94 |
2.48 |
35.73 |
60 |
| 1982年 |
10.08 |
2.30 |
22.82 |
34.49 |
| 1990年 |
11.33 |
1.80 |
15.88 |
22.21 |
| 1995年 |
12.07 |
1.45 |
12.01 |
16.58 |
| 2000年 |
12.9533 |
0.8507 |
6.57 |
8.72 |
请根据表中提供的信息, 画图表示全国人口总数的增长情况和全国文盲人口总数的下降情况.