四张小卡片上分别写有数字1、2、3、4.它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字2的概率;
(2)随机地从盒子里抽取一张.不放回再抽取第二张.请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.
某乳品公司最近推出一款果味酸奶,共有红枣、木瓜两种口味,若送奶员连续三天,每天从中任选一瓶某种口味的酸奶赠送给某住户品尝,则该住户收到的三瓶酸奶中,至少有两瓶为红枣口味的概率是多少?
(请用“画树状图”的方法给出分析过程,并求出结果)
某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错的题目进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:
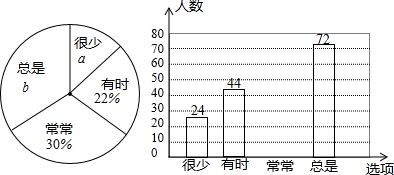
请根据图中信息,解答下列问题
(1)该调查的样本容量为 , , ,“常常”对应扇形的圆心角为
(2)请你补全条形统计图;
(3)若该校共有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名?
某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率分布表
|
活动次数 |
频数 |
频率 |
|
|
10 |
0.20 |
|
|
|
0.24 |
|
|
16 |
0.32 |
|
|
6 |
0.12 |
|
|
|
|
|
|
2 |
|
根据以上图表信息,解答下列问题:
(1)表中 , ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?

如图, ,以点 为圆心,1为半径画 与 的延长线交于点 ,过点 画 的垂线,垂线与 的一个交点为 ,连接
(1)线段 的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线 交于点 ,使线段 的长等于
②连 ,在 上画出点 ,使 的长等于 ,请写出画法,并说明理由.

一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、乙两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树状图或列表的方法列出所有可能的结果;
(2)这样的游戏规则是否公平?请说明理由.