图1中A和B是真空中的两块面积很大的平行金属板、加上周期为T的交流电压，在两板间产生交变的匀强电场。已知B板电势为零，A板电势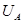
随时间变化的规律如图2所示，其中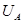的最大值为
，最小值为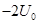
，在图1中，虚线MN表示与A、B板平行等距的一个较小的面，此面到A和B的距离皆为l。在此面所在处，不断地产生电量为q、质量为m的带负电的微粒，各个时刻产生带电微粒的机会均等。这种微粒产生后，从静止出发在电场力的作用下运动。设微粒一旦碰到金属板，它就附在板上不再运动，且其电量同时消失，不影响A、B板的电势，已知上述的T、、l、q和m等各量的值正好满足等式
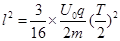。若不计重力，不考虑微粒间的相互作用，求：（结果用q、、m、T表示）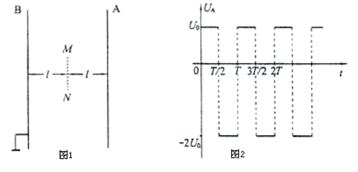
（1）在t=0到t=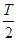
这段时间内产生的微粒中到达A板的微粒的最大速度
；
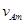（2）在0-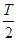范围内，哪段时间内产生的粒子能到达B板？
（3）在t=0到t=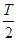这段时间内产生的微粒中到达B板的微粒的最大速度
；
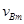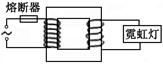
如下图所示，一个变压器（可视为理想变压器）的原线圈接在220V的市电上，向额定电压为18V的霓虹灯供电，使它正常发光。为了安全，需在原线圈回路中接入熔断器，若副线圈电路中电流超过12A时，熔丝就熔断。求变压器原副线圈匝数比。
熔丝的熔断电流是多大？
当副线圈电路中电流为10A时，变压器的输入功率是多大？
核发电在我们国家的技术已比较成熟，一个直径不足3米的圆球，一天能发100万度电，足够一个中型城市的工、农业需求。考虑到安全，应将其建在偏远山区。输电时，要考虑尽量减少输电线上的功率损失。有一个小型发电站，输送的电功率为P=1000kw，输电线电阻为当使用U=5kv的电压输电时，测得安装在输电线路起点和终点处的两只电度表一昼夜示数相差8000度。
求：这时的输电效率η和输电线的总电阻r。
若想使输电效率提高到98%，又不改变输电线，那么电站应使用多高的电压向外输电？
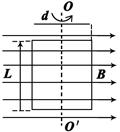
如下图所示，匀强磁场磁感应强度B=0.5T，匝数为n=50匝的矩形线圈，绕垂直于匀强磁场的转轴OO′匀速转动，每匝线圈长为L=25cm，宽为d=20cm，线圈每分钟转动1500r，在匀速转动过程中，从线圈平面经过图示位置时开始计时。写出交流感应电动势e的瞬时值表达式；
若每匝线圈本身电阻r=0.02Ω，外接一阻值为13Ω的用电器，使线圈与外电路组成闭合电路，写出交流感应电流i的瞬时值表达式；
若从线圈平面垂直于磁感线的位置开始计时，感应电动势e′和感应电流i′的瞬时表达式如何？
一台小型发电机产生的电动势随时间变化的正弦规律图象如下图甲所示。已知发电机线圈内阻为5.0Ω，则外接一只电阻为95.0Ω的灯泡，如下图乙所示。
求：电压表的示数；
发电机线圈内阻每秒钟产生的焦耳热；
若发电机是单匝线圈，通过线圈的最大磁通量。
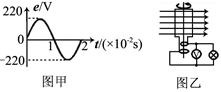
如下图（a）所示，间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场，磁感应强度为B；在区域Ⅱ内有垂直于斜面向下的匀强磁场，其磁感应强度Bt的大小随时间t变化的规律如下图（b）所示。t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑，同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放。在ab棒运动到区域Ⅱ的下边界EF处之前，cd棒始终静止不动，两棒均与导轨接触良好。已知cd棒的质量为m、电阻为R，ab棒的质量、阻值均未知，区域Ⅱ沿斜面的长度为2l，在t=tx时刻（tx未知）ab棒恰进入区域Ⅱ，重力加速度为g。求：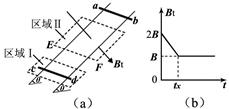
通过cd棒电流的方向和区域I内磁场的方向；
当ab棒在区域Ⅱ内运动时cd棒消耗的电功率；
ab棒开始下滑的位置离EF的距离；
ab棒开始下滑至EF的过程中回路中产生的热量。