（1）在物理学发展史上，许多科学家通过恰当应用科学研究方法，超越了当时研究条件的局限和传统观念，取得了辉煌的研究成果，下列符合物理学史实的是
A．牛顿由理想斜面实验通过逻辑推理否定了力是维持物体运动的原因的观点。
B．19世纪以前，对相隔一定距离的电荷或磁体间的作用不少人持超距作用的观点，在19世纪30年代，法拉第提出电场或磁场的观点。
C．人们从电荷间的作用力与引力的相似性中提出“平方反比”的猜想，这一科学问题是由法国科学家库仑通过库仑扭秤实验完成的
D．安培首先引入电场线和磁感线，极大地推动了电磁现象的研究。
E．牛顿通过著名的“月地检验”，突破天地之间的束缚，使得万有引力定律成为科学史上最伟大定律之一。
（2）微波实验是近代物理实验室中的一个重要部分．反射式速调管是一种结构简单、实用价值较高的常用微波器件之一，它是利用电子团与场相互作用在电场中发生振荡来产生微波，其振荡原理与下述过程类似．如图1所示，在虚线MN两侧分布着方向平行于x轴的电场，其电势φ随x的分布可简化为如图2所示的折线．一带电微粒从A点由静止开始，在电场力作用下沿直线在A、B两点间往返运动．已知带电微粒质量m=1.0×10﹣20 kg，带电荷量q=﹣1.0×10﹣9 C，A点距虚线MN的距离d1=1.0cm，不计带电微粒的重力，忽略相对论效应．求：
①B点距虚线MN的距离d2；
②带电微粒在A、B之间震荡的周期T．
在水平地面上方的足够大的真空室内存在着匀强电场和匀强磁场共存的区域，且电场与磁场的方向始终平行，在距离水平地面的某一高度处，有一个带电量为q、质量为m的带负电的质点，以垂直于电场方向的水平初速度v0进入该真空室内，取重力加速度为g。求：
（1）若要使带电质点进入真空室后做半径为R的匀速圆周运动，求磁感应强度B0的大小及所有可能的方向；
（2）当磁感应强度的大小变为B时，为保证带电质点进入真空室后做匀速直线运动，求此时电场强度E的大小和方向应满足的条件；
（3）若带电质点在满足第（2）问条件下运动到空中某一位置M点时立即撤去磁场，此后运动到空中另一位置N点时的速度大小为v，求M、N两点间的竖直高度H及经过N点时重力做功的功率。
如图所示，质量为M的铁箱内装有质量为m的货物．以某一初速度向上竖直抛出，上升的最大高度为H，下落过程的加速度大小为a，重力加速度为g，铁箱运动过程受到的空气阻力大小不变．求：
（1）铁箱下落过程经历的时间；
（2）铁箱和货物在落地前的运动过程中克服空气阻力做的功；
（3）上升过程货物受到铁箱的作用力．
如图，C1D1E1F1和C2D2E2F2是距离为L的相同光滑导轨，C1D1和E1F1为两段四分之一圆弧，半径分别为r1=8r和r2=r。在水平矩形D1E1E2D2内有竖直向上的匀强磁场，磁感应强度为B。导体棒P、Q的长度均为L，质量均为m，电阻均为R，其余电阻不计，Q停在图中位置，现将P从轨道最高点无初速释放，则
（1）求导体棒P进入磁场瞬间，回路中的电流的大小和方向（顺时针或逆时针）；
（2）若P、Q不会在轨道上发生碰撞，棒Q到达E1E2瞬间，恰能脱离轨道飞出，求导体棒P离开轨道瞬间的速度；
（3）若P、Q不会在轨道上发生碰撞，且两者到达E1E2瞬间，均
能脱离轨道飞出，求回路中产生热量的范围。
如图所示，水平台高h=0.8m，台上A点放有一大小可忽略的滑块，质量m=0.5kg，滑块与台面间的动摩擦因数μ=0.5；现对滑块施加一个斜向上的拉力F=5N，θ=37°，经t1=1s，滑块到达平台上B点时撤去拉力，滑块继续运动，最终落到地面上的D点，x=0.4m。（取sin37°=0.6，cos37°=0.8，g=10m/s2）
（1）求滑块在C点离开台面瞬间的速度；
（2）滑块在AB段的加速度大小；
（3）求AC间的距离。
如图20所示，质量为m、边长为L的正方形线框，从有界匀强磁场上方、离磁场边界h处由静止开始下落（下落过程中线圈下边始终保持水平，不计空气阻力）。线框每边电阻为R，匀强磁场的宽度为H（H>L）、磁感应强度为B，重力加速度为g。试求：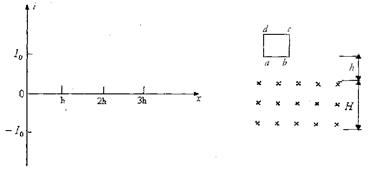
（1）当线圈的ab边刚进入磁场时，它可能做什么运动，并分析各种运动下h的条件．
（2）设ab边刚进入磁场和刚穿出磁场时都作减速运动，且加速度大小相等。求线框经
过磁场的过程中产生的焦耳热。
（
3）设线圈刚好以匀速运动进入匀强磁场，此时线圈中的电流为I0，且线圈的边长L=h磁场的宽度H=2h。请在坐标系中定性画出线圈进入磁场到离开磁场的过程中，线圈中的电流i随下落高度x变化的图象。（不需要计算过程，设
电流沿abcda如方向为正方向，x以磁场上边界为起点。）