在直角坐标系 中,以
中,以 为极点,
为极点, 轴正半轴为极轴建立极坐标系.圆
轴正半轴为极轴建立极坐标系.圆 ,直线
,直线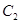 的极坐标方程分别为
的极坐标方程分别为 .
.
(Ⅰ)求 与
与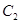 交点的极坐标;
交点的极坐标;
(Ⅱ)设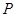 为
为 的圆心,
的圆心, 为
为 与
与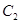 交点连线的中点.已知直线
交点连线的中点.已知直线 的参数方程为
的参数方程为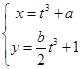 (
(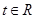 为参数),求
为参数),求 的值.
的值.
已知函数 .
.
(1)设 ,且
,且 ,求
,求 的值;
的值;
(2)在△ABC中,AB=1, ,且△ABC的面积为
,且△ABC的面积为 ,求sinA+sinB的值.
,求sinA+sinB的值.
对有 个元素的总体
个元素的总体 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体 和
和 (
( 是给定的正整数,且
是给定的正整数,且 ),再从每个子总体中各随机抽取
),再从每个子总体中各随机抽取 个元素组成样本.用
个元素组成样本.用 表示元素
表示元素 和
和 同时出现在样本中的概率.
同时出现在样本中的概率.
(1)求 的表达式(用
的表达式(用 表示);
表示);
(2)求所有 的和.
的和.
如图所示的几何体中,面 为正方形,面
为正方形,面 为等腰梯形,
为等腰梯形, ,
, ,
, ,且平面
,且平面
 平面
平面 .
.
(1)求 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)线段 上是否存在点
上是否存在点 ,使平面
,使平面
 平面
平面 ?
?
证明你的结论.
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系 的
的 点为极点,
点为极点, 轴正方向为极轴,且长度单位相同,建立极坐标系,得直线
轴正方向为极轴,且长度单位相同,建立极坐标系,得直线 的极坐标方程为
的极坐标方程为 .求直线
.求直线 与曲线
与曲线 交点的极坐标.
交点的极坐标.
已知矩阵 ,点
,点 ,
,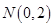 .求线段
.求线段 在矩阵
在矩阵 对应的变换作用下得到线段
对应的变换作用下得到线段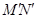 的长度.
的长度.