(满分14分)已知函数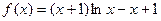 .
.
(1)若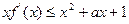 ,求a的取值范围;
,求a的取值范围;
(2)证明: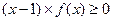 .
.
(满分12分)已知n是大于1的自然数,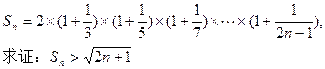
(满分12分)某同学参加3门课程的考试.假设该同学第一门课程取得优秀的概率是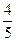 ,第二、第三门课程取得优秀成绩的概率分别是p,q(p>q),且不同课程是否取得优秀成绩相互独立,记X为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别是p,q(p>q),且不同课程是否取得优秀成绩相互独立,记X为该生取得优秀成绩的课程数,其分布列为
| X |
0 |
1 |
2 |
3 |
| P |
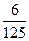 |
a |
b |
 |
(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求p,q的值;
(3)求数学期望E(X).
(满分12分)已知二项式 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求 的值;
的值;
(2)设 .
.
①求 的值; ②求
的值; ②求 的值.
的值.
(满分12分)从1,3,5,7,9中任取三个数字,从2,4,6,8中任取两个数字,可以组成多少:(列出式子并用数字给出最后答案)
(1)无重复数字的五位数;
(2)万位、百位和个位数字是奇数的无重复数字的五位数;
(3)千位和十位数字只能是奇数的无重复数字的五位数.