如图所示xOy平面内，在x轴上从电离室产生的带正电的粒子，以几乎为零的初速度飘入电势差为U=200V的加速电场中，然后经过右侧极板上的小孔沿x轴进入到另一匀强电场区域，该电场区域范围为﹣l≤x≤0（l=4cm），电场强度大小为E=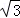
×104V/m，方向沿y轴正方向．带电粒子经过y轴后，将进入一与y轴相切的圆形边界匀强磁场区域，磁场区域圆半径为r=2cm，圆心C到x轴的距离为d=4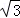cm，磁场磁感应强度为B=8×10﹣2T，方向垂直xoy平面向外．带电粒子最终垂直打在与y轴平行、到y轴距离为L=6cm的接收屏上．求：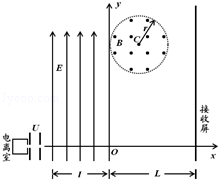
（1）带电粒子通过y轴时离x轴的距离；
（2）带电粒子的比荷；
（3）若另一种带电粒子从电离室产生后，最终打在接收屏上y=
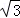cm处，则该粒子的比荷又是多少？
一物体做匀加速直线运动，初速度为0.5m/s，第7s内的位移比第5s内的位移多4m，求：
（1）物体的加速度；
（2）物体在5s内的位移．
测速仪安装有超声波发射和接收装置，如图所示，B为测速仪，A为汽车，两者相距335m，某时刻B发出超声波，同时A由静止开始做匀加速直线运动．当B接收到反射回来的超声波信号时，A、B相距355m，已知声速为340m/s，求汽车的加速度大小．
汽车在平直的公路上以30m/s的速度匀速行驶，开始刹车后又以5m/s2的加速度做匀减速直线运动，求：
（1）从开始刹车后10秒钟汽车前进了多少米？
（2）静止前4s内汽车滑行的位移多大？
一火车以2m/s的初速度，0.5m/s2的加速度做匀加速直线运动，求：
（1）火车在第3s末的速度是多少？
（2）5s内的位移是多少？
甲乙两辆汽车都从静止出发做加速直线运动，加速度方向一直不变．在第一段时间间隔内，两辆汽车的加速度大小不变，汽车乙的加速度大小是甲的两倍；在接下来的相同时间间隔内，汽车甲的加速度大小增加为原来的两倍，汽车乙的加速度大小减小为原来的一半．求甲乙两车各自在这两段时间间隔内走过的总路程之比．