如图,椭圆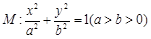 的离心率为
的离心率为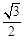 ,直线
,直线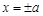 和
和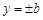 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.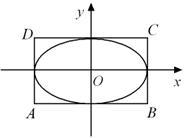
(1)求椭圆M的标准方程;
(2)设直线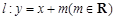 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点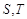 .求
.求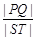 的最大值及取得最大值时
的最大值及取得最大值时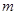 的值.
的值.
对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为: )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为 (1≤a≤3).设用
(1≤a≤3).设用 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是 (
(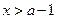 ),用
),用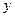 质量的水第二次清洗后的清洁度是
质量的水第二次清洗后的清洁度是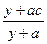 ,其中
,其中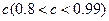 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.
(Ⅰ)分别求出方案甲以及 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当 为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论
为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
求 的值。
的值。
一个扇形 的周长为
的周长为 ,求扇形的半径,圆心角各取何值时,此扇形的面积最大?
,求扇形的半径,圆心角各取何值时,此扇形的面积最大?
角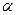 的终边上的点
的终边上的点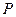 与
与 关于
关于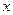 轴对称
轴对称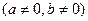 ,角
,角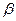 的终边上的点
的终边上的点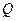 与
与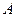 关于直线
关于直线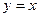 对称,求
对称,求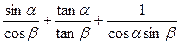 之值.
之值.
已知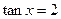 ,(1)求
,(1)求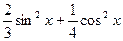 的值。
的值。
(2)求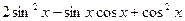 的值。
的值。