（本小题满分12分）
如图，已知正三棱柱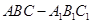
各棱长都是4，
是
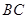的中点，动点
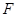在侧棱
上，且不与点
重合．
（Ⅰ）当
时，求证：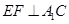
；
（Ⅱ）设二面角
的大小为
，求
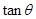的最小值．
如图，海中有一小岛，周围
海里内有暗礁.一军舰从A地出发由西向东航行，望见小岛B在北偏东75°，航行8海里到达C处，望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进，问此舰有没有触礁的危险
集合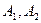
满足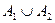
=A，则称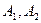（）为集合A的一种分拆，并规定：当且仅当
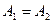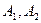时，（）与（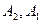
）为集合A的同一种分拆，则集合A={
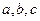}的不同分拆种数为多少？
在某次数学竞赛中共有甲、乙、丙三题，共25人参加竞赛，每个同学至少选作一题。在所有没解出甲题的同学中，解出乙题的人数是解出丙题的人数的2倍；解出甲题的人数比余下的人数多1人；只解出一题的同学中，有一半没解出甲题，问共有多少同学解出乙题？
已知全集
，若
，
，
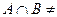
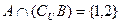，试写出满足条件的A、B集合.
设集合
，
，
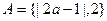，求实数a的值.