如图,在四棱锥P-ABCD中,平面PAD⊥底面 ABCD,侧棱PA=PD=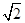 ,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)线段AD上是否存在点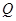 ,使得它到平面PCD的距离为
,使得它到平面PCD的距离为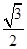 ?若存在,求出
?若存在,求出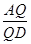 值;若不存在,请说明理由.
值;若不存在,请说明理由.
如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.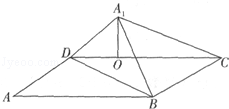

(Ⅰ)求证:BC⊥A1D;
(Ⅱ)求证:平面A1CD⊥平面A1BC;
(Ⅲ)若AB=10,BC=6,求三棱锥A1﹣BCD的体积.
已知数列{an}是等比数列,首项a1=1,公比q>0,其前n项和为Sn,且S1+a1,S3+a3,S2+a2成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足 ,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
已知函数f(x)=|x-1|+|x-a|.
(1)当a=2时,解不等式f(x)≥4;
(2)若不等式f(x)≥a恒成立,求实数a的取值范围.
已知函数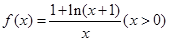 .
.
(Ⅰ)函数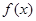 在区间
在区间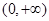 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;
(Ⅱ)当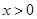 时,
时, 恒成立,求整数
恒成立,求整数 的最大值;
的最大值;
(Ⅲ)试证明: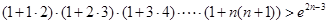 .
.