设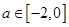 ,已知函数
,已知函数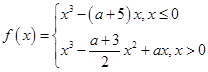 ,
,
(1)证明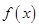 在区间
在区间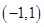 内单调递减,在区间
内单调递减,在区间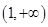 内单调递增;
内单调递增;
(2)设曲线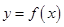 在点
在点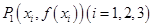 处的切线相互平行,且
处的切线相互平行,且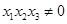 ,
,
证明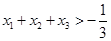
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(1)求函数g(x)的解析式;
(2)解不等式g(x)≥f(x)-|x-1|;
(3)若h(x)=g(x)-λf(x)+1在[-1,1]上是增函数,求实数λ的取值范围
某企业生产一种产品时,固定成本为5000元,而每生产100台产品时直接消耗成本要增加2500元,市场对此商品年需求量为500台,销售的收入函数为R(x)=5x-x2(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台)
(1)把利润表示为年产量的函数;
(2)年产量多少时,企业所得的利润最大?
(3)年产量多少时,企业才不亏本?
若函数y=f(x)=x2-2x+4的定义域、值域都是闭区间[2,2b],求b的值.
已知α,β是方程4x2-4tx-1=0(t∈R)的两个实数根,函数f(x)=的定义域为[α,β].
(1)判断f(x)在[α,β]上的单调性,并证明你的结论;
(2)设g(t)=maxf(x)-minf(x),求函数g(t)的最小值
已知函数f(x)在(-1,1)上有定义,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f,试证明:
(1)f(x)为奇函数;
(2)f(x)在(-1,1)上单调递减.