已知函数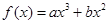 在点
在点 处的切线方程为
处的切线方程为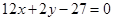 ,且对任意的
,且对任意的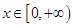 ,
,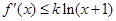 恒成立.
恒成立.
(Ⅰ)求函数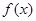 的解析式;
的解析式;
(Ⅱ)求实数 的最小值;
的最小值;
(Ⅲ)求证: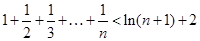 (
(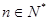 ).
).
三棱锥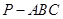 ,底面
,底面 为边长为
为边长为 的正三角形,平面
的正三角形,平面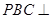 平面
平面 ,
,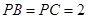 ,
,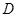 为
为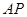 上一点,
上一点,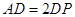 ,
,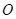 为底面三角形中心.
为底面三角形中心. 
(Ⅰ)求证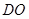 ∥面
∥面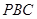 ;
;
(Ⅱ)求证: ;
;
(Ⅲ)设 为
为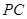 中点,求二面角
中点,求二面角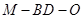 的余弦值.
的余弦值.
已知数列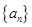 ,
, ,
,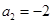 ,记
,记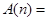
 ,
,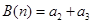
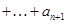 ,
,
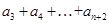 (
(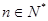 ),若对于任意
),若对于任意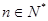 ,
,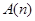 ,
, ,
, 成等差数列.
成等差数列.
(Ⅰ)求数列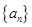 的通项公式;
的通项公式;
(Ⅱ) 求数列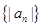 的前
的前 项和.
项和.
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛. 该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为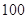 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
| 分数(分数段) |
频数(人数) |
频率 |
| [60,70) |
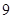 |
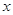 |
| [70,80) |
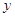 |
 |
| [80,90) |
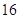 |
 |
| [90,100) |
 |
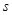 |
| 合计 |
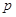 |
 |
(Ⅰ)求出上表中的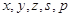 的值;
的值;
(Ⅱ)按规定,预赛成绩不低于 分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一·二班在决赛中进入前三名的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
在 中,角
中,角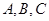 所对应的边分别为
所对应的边分别为 ,
,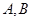 为锐角且
为锐角且 ,
,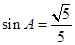 ,
, .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若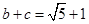 ,求
,求 的值.
的值.