已知数列{an}的各项均为正数的等比数列，且a1a2=2，a3a4=32，
（1）求数列{an}的通项公式；
（2）设数列{bn}的前n项和为Sn=n2，（n∈N*）,求数列{anbn}的前n项和Tn.
请考生在22、23两题中任选一题作答，如果都做，则按所做的第一题记分。
（本小题满分10分）选修4-1：几何证明选讲
如图，AB是⊙O的直径，C、F为⊙O上的点，CA是∠BAF的角平分线，过点C
作CD⊥AF交AF的延长线于D点，CM⊥AB，垂足为点M。
（I）求证：DC是⊙O的切线； （II）求证：AM：MB=
DF·DA。
（本小题满分12分）
已知函数
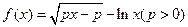是增函数。
（I）求实数p的取值范围；
（II）设数列
的通项公式为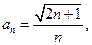
前n项和为S，求证：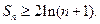
（本小题满分12分）
已知圆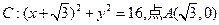
，Q是圆上一动点，AQ的垂直平分线交CQ于点M，设点M的轨迹为E。
（I）求轨迹E的方程；
（II）过点P（1，0）的直线
交轨迹E于两个不同的点A、B，
（O是坐标原点）的面积
，若弦AB的中点为R，求直线OR斜率的取值范围。
（本小题满分12分）
如图，正方形ADEF和等腰梯形ABCD垂直，已知BC=2AD=4，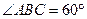
，
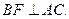
（I）求证：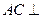
面ABF；
（II）求异面直线BE与AC所成的角的余弦值；
（III）在线段BE上是否存在一点P，使得平面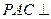
平面BCEF？若存在，求出
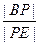的值，若不存在，请说明理由。
（本小题满分12分）
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度：在C处进行该仪器的垂直弹射，观测点A、B两地相距100米，
，在A地听到弹射声音的时间比B地晚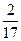
秒，A地测得该仪器在C处时的俯角为15°A地测得最高点H时的仰角为30°，求该仪器的垂直弹射高度CH（声音的传播速度为340米/秒）