已知:x1,x2,…x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1= ,则
,则 = ;
= ;
(2)若y2= ,则
,则 = ;
= ;
(3)若y3= ,则
,则 = ;
= ;
(4)由以上探究可知,y2012= ,
, 共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
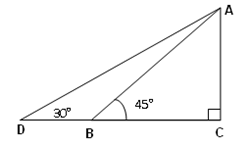
如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜角由45º降为30º,已知原滑滑板AB的长为5米,点D、B、C在同一水平地面上.改善后滑滑板会加长多少?(精确到0.01)
若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?说明理由。
(参考数据: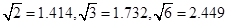 )
)
如图,在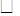 ABCD中,
ABCD中,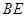 平分
平分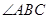 交
交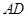 于点
于点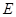 ,
,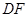 平分
平分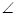
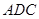 交
交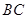 于点
于点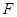 。
。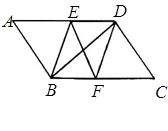
求证:
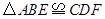
若
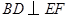 ,则判断四边形
,则判断四边形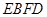 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论.
如图,甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为m,乙转盘中指针所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区域为止).
请你用画树状图或列表格的方法求出|m+n|>1的概率;
直接写出点(m,n)落在函数y=-图象上的概率.
为了提高农民抵御大病风险的能力,全国农村推行了新型农村合作医疗政策,农民只需每人每年交20元钱,就可以加入合作医疗.若农民患病住院治疗,出院后到新型农村合作医疗办公室按一定比例报销医疗费.小军与同学随机调查了他们镇的一些村民,根据收集到的数据绘制成了如图所示的统计图.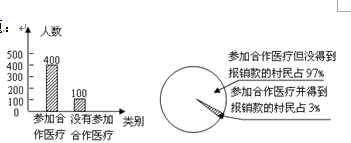
根据以上信息,解答下列问题本次共调查了多少村民?被调查的村民中,有多少人参加合作医疗得到了报销款?
若该镇有村民12500人,请你计算有多少人参加了合作医疗?要使两年后参加作医疗的人数增加到12100人,假设这两年的年增长率相同,求这个年增长率
先化简:
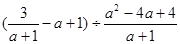 ,并从0,
,并从0, ,2中选一个合适的数作为
,2中选一个合适的数作为 的值代入求值.
的值代入求值.