小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：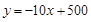
，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的80%．
（1）设小明每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．
（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？
（3）如果小明想要每月获得的利润为2000元，那么小明每月的成本需要多少元？（成本＝进价×销售量）
计算：
（1）求
的值：
．
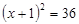（2）计算：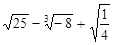
；
【改编】某班同学在植树节这天参加了植树活动，已知男生比女生少4人，男生每人种3棵，女生每人种2棵，并且男女生所种树木棵数相同，设男生有x人，女生有y人，根据题意，列方程组正确的是（）
A． |
B． |
C． |
D． |
【原创】（1）已知：如图1，BE⊥DE，∠1=∠B，∠2=∠D，试确定AB与CD的位置关系，并说明理由.
（2）若图形变化为如图2、图3所示，且满足∠1+∠2=90°，那么AB与CD还满足上述关系吗？若满足，选择一个图形进行证明.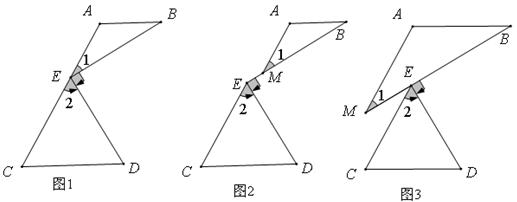
（本题7分）某中学新建了一栋四层的教学楼，每层楼有10间教室，进出这栋教学楼共有4个门，其中两个正门大小相同，两个侧门大小也相同.安全检查中，对4个门进行了测试，当同时开启一个正门和两个侧门时，2分钟内可以通过560名学生；当同时开启一个正门和一个侧门时，4分钟内可以通过800名学生.
（1）求平均每分钟开启一个正门和一个侧门各可以通过多少名学生？
（2）检查中发现，出现紧急情况时，因学生拥挤，出门的效率将降低20%，安全检查规定：在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离，假设这栋教学大楼每间教室最多有45名学生，问：该教学楼建造的这4个门是否符合安全规定？请说明理由.
阅读下面的文字，解答问题：
大家知道
是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，但是由于
，所以的整数部分为1，将减去其整数部分1，所得的差就是其小数部分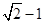
，根据以上的内容，解答下面的问题：
（1）
的整数部分是________，小数分部是________；
（2）
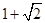的整数部分是________，小数小数分部是________；
（3）若设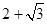
整数部分是
小数部分是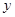
，求
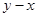的值．