已知二次函数 的图象C1与x轴有且只有一个公共点.
的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(—3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
如图,已知,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=400,求∠2的度数.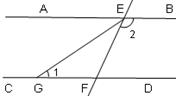
如图①是长方形纸带,将纸带沿EF折叠成图②,再沿BF折叠成图③.
(1)若∠DEF=200,则图③中∠CFE度数是多少?
(2)若∠DEF=α,把图③中∠CFE用α表示.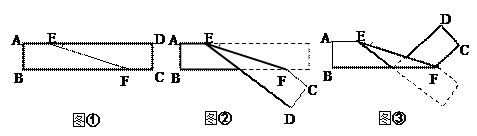
某中学拟组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”
小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?
如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?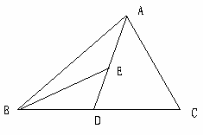
如图,已知∠ABC.请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边与点P.探究:∠ABC 与 ∠DEF 有怎样的数量关系?并说明理由(需要证明).