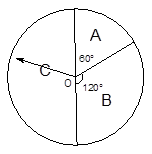(本小题满分10分)选修4-4:坐标系与参数方程
已知直线的极坐标方程为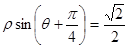 ,圆
,圆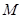 的参数方程为
的参数方程为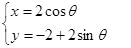 (其中
(其中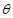 为参数).
为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆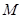 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
(本小题满分10分)选修4-1几何证明选讲
如图,在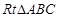 中,
中, ,
, 平分
平分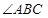 交
交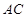 于点
于点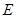 ,点
,点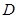 在
在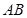 上,
上,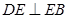 .
.
(1)求证: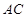 是△
是△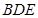 的外接圆的切线;
的外接圆的切线;
(2)若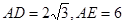 ,求
,求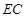 的长.
的长.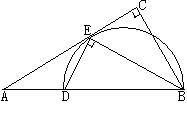
(本小题满分12分)已知函数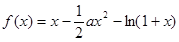 ,其中
,其中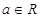 .
.
(Ⅰ)若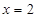 是
是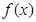 的极值点,求
的极值点,求 的值;
的值;
(Ⅱ)求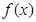 的单调区间;
的单调区间;
(Ⅲ)若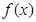 在
在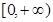 上的最大值是
上的最大值是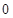 ,求
,求 的取值范围 .
的取值范围 .
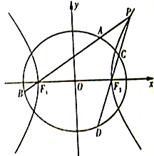
(本小题满分12分)如图,已知椭圆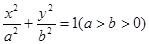 的离心率为
的离心率为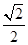 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点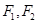 为顶点的三角形的周长为
为顶点的三角形的周长为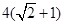 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设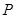 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线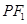 和
和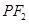 与椭圆的交点分别为
与椭圆的交点分别为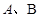 和
和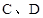 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线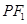 、
、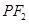 的斜率分别为
的斜率分别为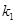 、
、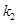 ,证明
,证明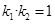 ;
;
(Ⅲ)是否存在常数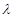 ,使得
,使得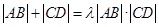 恒成立?若存在,求
恒成立?若存在,求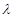 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的以 为圆心的转盘一次,并获得相应金额的返券,假定指针等可能地指向任一位置(不指向各区域的边界). 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
为圆心的转盘一次,并获得相应金额的返券,假定指针等可能地指向任一位置(不指向各区域的边界). 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(Ⅰ)若某位顾客消费128元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为 (元).求随机变量
(元).求随机变量 的分布列和数学期望.
的分布列和数学期望.