如图所示,竖直平面内有四分之一圆弧轨道固定在水平桌面上,圆心为O点。一小滑块自圆弧轨道A处由静止开始自由滑下,在B点沿水平方向飞出,落到水平地面C点。已知小滑块的质量为m=1.0kg,C点与B点的水平距离为1m,B点高度为1.25m,圆弧轨道半径R=1m,g取10m/s2。求小滑块:
(1)从B点飞出时的速度大小;
(2)在B点时对圆弧轨道的压力大小;
(3)沿圆弧轨道下滑过程中克服摩擦力所做的功。
如图所示,匀强磁场B="0.1" T,金属棒AD长0.4 m,与框架宽度相同,其电阻为R= Ω,框架电阻不计,电阻R1="2" Ω,R2="1" Ω,当金属棒以5 m/s的速度匀速向左运动时,求:
(1)流过金属棒的感应电流多大?
(2)若图中电容器C为0.3 μF,则带多少电荷量?
设想有一宇航员在某未知星球的极地地区着陆时发现,同一物体在该地区的重力是地球上的重力的0.01倍.还发现由于星球的自转,物体在该星球赤道上恰好完全失重,且该星球上一昼夜的时间与地球上相同。则这未知星球的半径是多少?(取地球上的重力加速度 g=9.8 m/s2,π2=9.8,结果保留两位有效数字)
如图为“快乐大冲关”节目中某个环节的示意图,参与游戏的选手会遇到一个人造山谷AOB,AO是高h=3 m的竖直峭壁,OB是以A点为圆心的弧形坡,∠OAB=60°,B点右侧是一段水平跑道.选手可以自A点借助绳索降到O点后再爬上跑道,但身体素质好的选手会选择自A点直接跃上跑道.选手可视为质点,忽略空气阻力,重力加速度g=10 m/s2。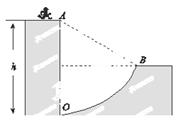
(1)若选手以速度v0水平跳出后,能跳在水平跑道上,求v0的最小值;
(2)若选手以速度v1=4 m/s水平跳出,求该选手在空中的运动时间。
轻杆长L=1.5m,以一端为圆心,在竖直面内做圆周运动,杆另一端固定一个质量m=1.8kg小球,小球通过最高点时速率v=3m/s,求此时小球对杆的作用力大小及方向(g=10m/s2)。
长为L的细线,拴一质量为m的小球,一端固定于O点。让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示。当摆线L与竖直方向的夹角是 时,求:
时,求:
(1)线的拉力F;
(2)小球运动的线速度大小;