某车间生产一种仪器的固定成本是
元，每生产一台该仪器需要增加投入
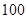元，已知总收入满足函数：
，其中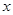
是仪器的月产量．（利润＝总收入－总成本）．
（Ⅰ）将利润表示为月产量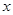的函数；
（Ⅱ）当月产量为何值时，车间所获利润最大？最大利润是多少元？
(本题满分14分
)
已知向量
，
（其中
为正常数）
（Ⅰ）若
，求
时
的值；
（Ⅱ）设
，若函数
的图像的相邻两个对称中心的距离为
，求在区间
上的最小值。
（1）（本小题满分7分）
选修4-4：矩阵与变换
已知矩阵
,A的一个特征值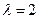
，其对应的特征向量是
.
（Ⅰ）求矩阵
；
（Ⅱ）求直线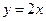
在矩阵M所对应的线性变换下的像的方程
（2）
（本小题满分7分）选修4-4：坐标系与参数方程
已知曲线C的极坐标方程是
．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：
，
求直线l与曲线C相交所成的弦的弦长．
（（3）（本小题满分7分）
选修4-5：不等式选讲解不等式∣2x-1∣<∣x∣+1
（本小题满分14分）
已知函数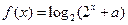
（a为常数）是R上的奇函数，函数
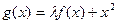是区间[-1，1]上的减函数.
（I）求a的值；
（II）若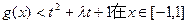
上恒成立，求t的取值范围；
（III）讨论关于x的方程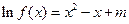
解的情况，并求出相应的m的取值范围.
（本小题满分13分）
如图，ABCD是块矩形硬纸板，其中AB=2AD= 2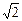
，E为DC中点，将它沿AE折成直二面角D-AE-B.
（Ⅰ）求证：AD⊥平面BDE；
（Ⅱ）求二面角B-AD-E的余弦值.
（本小题满分13分）
某班从6名班干部（其中男生4人，女生2人）中选3人参加学校学生会的干部竞选．
（Ⅰ）设所选3人中女生人数为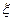
，求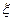的分布列及数学期望
；
（Ⅱ）在男生甲被选中的情况下，求女生乙也被选中的概率．