如图,已知海岛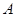 到海岸公路
到海岸公路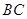 的距离
的距离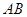 为50km,
为50km,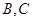 间的距离为100km,从
间的距离为100km,从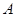 到
到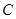 ,
,
必须先坐船到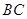 上的某一点
上的某一点 ,船速为
,船速为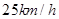 ,再乘汽车到
,再乘汽车到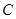 ,车速为
,车速为 ,记
,记 .
.
(1)试将由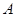 到
到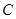 所用的时间
所用的时间 表示为
表示为 的函数
的函数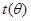 ;
;
(2)问 为多少时,由
为多少时,由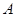 到
到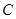 所用的时间
所用的时间 最少?
最少?
双曲线M的中心在原点,并以椭圆 的焦点为焦点,以抛物线
的焦点为焦点,以抛物线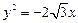 的准线为右准线.
的准线为右准线.
(1)求双曲线M的方程;
(2)设直线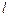 :
: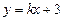 与双曲线M相交于A、B两点,O是原点.
与双曲线M相交于A、B两点,O是原点.
① 当 为何值时,使得
为何值时,使得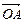

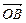
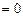 ?
?
② 是否存在这样的实数 ,使A、B两点关于直线
,使A、B两点关于直线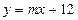 对称?若存在,求出
对称?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,在长方体 中,
中, 点
点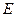 在棱
在棱 上移动.
上移动.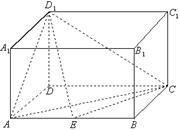 (1)证明:
(1)证明: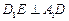 ;
;
(2)若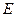 为
为 中点,求
中点,求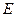 到面
到面 的距离;
的距离;
(3)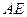 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为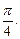
在△ABC中,角A、B、C所对的边分别是 且
且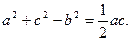
(1)求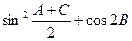 的值;
的值;
(2)若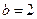 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
设函数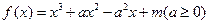 .
.
(1)求函数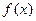 的单调区间;
的单调区间;
(2)若函数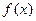 在
在 内没有极值点,求
内没有极值点,求 的取值范围;
的取值范围;
(3)若对任意的 ,不等式
,不等式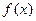 ≤
≤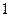 在
在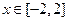 上恒成立,求
上恒成立,求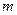 的取值范围.
的取值范围.
已知函数 ,数列
,数列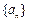 满足
满足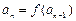 (n≥2,nÎN*).
(n≥2,nÎN*).
若 ,数列
,数列 满足
满足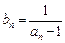
(1)求证:数列 是等差数列;
是等差数列;
(2)设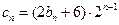 ,求数列
,求数列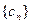 的前n项和
的前n项和 。
。