七年级我们学过三角形的相关知识，在动手实践的过程中，发现了一个基本事实：
三角形的三条高（或三条高所在直线）相交于一点．
其实，有很多八年级、九年级的问题均可用此结论解决．
【运用】如图，已知：△ABC的高AD与高BE相交于点F，且∠ABC=45°，过点F作FG∥BC交AB于点G，求证：FG+CD=BD．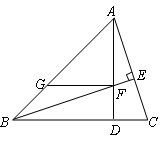
小方同学在解答此题时，利用了上述结论，她的方法如下：
连接CF并延长，交AB于点M，
∵△ABC的高AD与高BE相交于点F，
∴CM为△ABC的高．
（请你在下面的空白处完成小方的证明过程．）
【操作】如图AB是圆的直径，点C在圆内，请仅用无刻度的直尺画出△ABC中AB边上的高．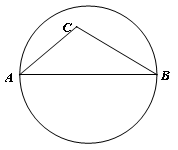
从甲学校到乙学校有
、
、
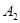三条线路，从乙学校到丙学校有
、
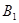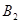二条线路。
（1）利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果；
（2）小张任意走了一条从甲学校到丙学校的线路，求小张恰好经过了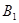线路的概率是多少？
已知方程
则 ①当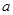
取什么值时，方程有两个不相等的实数根？②当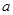取什么值时，方程有两个相等的实数根？③、当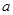取什么值时，方程没有实数根？
如图，
ABCD，四个内角平分线相交于E、F、G、H。求证：四边形EFGH是矩形。
方程
；
（1）
取何值时是一元二次方程，并求出此方程的解；
（2）取何值时是一元一次方程；
如图，在四边形 ABCD 中，AB = CD，M、N、E、F 分别为 AD、BC、BD、AC 的中点，
求证：四边形 MENF为菱形。