从甲学校到乙学校有 、
、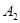 、
、 三条线路,从乙学校到丙学校有
三条线路,从乙学校到丙学校有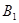 、
、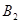 二条线路。
二条线路。
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了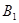 线路的概率是多少?
线路的概率是多少?
小明和小刚一起做游戏,游戏规则如下:将分别标有数字1,2,3,4的4个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
(1)化简: ;
(2)解不等式组 ,并写出它的正整数解.
请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知: ,直线 及 上两点 , .
求作: ,使点 在直线 的上方,且 , .

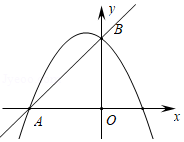
在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过点 、 .
(1)求 、 满足的关系式及 的值.
(2)当 时,若 的函数值随 的增大而增大,求 的取值范围.
(3)如图,当 时,在抛物线上是否存在点 ,使 的面积为1?若存在,请求出符合条件的所有点 的坐标;若不存在,请说明理由.
如图,在正方形 中, 是 边上一点,(与 、 不重合),连接 ,将 沿 所在的直线折叠得到 ,延长 交 于 ,连接 ,作 ,与 的延长线交于点 ,连接 .显然 是 的平分线, 是 的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于 的角平分线),并说明理由.
