一个正方形的一边增加3cm,相邻一边减少3cm,所得矩形面积与这个正方形的每边减去1cm所得的正方形面积相等,求这矩形的长与宽.
已知关于x的方程4x+2m+1=2x+5。
(1)若方程的解为x=-2,求m的值;
(2)若方程的解是负数,求m的取值范围。
完成一项工作,如果由一个人单独做要花45小时,现先由一部分人做一小时,随后增加15人和他们一起又做了两小时,恰好完成.假设每个人的工作效率相同,那么先安排做的人数是多少?
(1)化简: 4(2x2 xy)
xy) (x2+xy
(x2+xy 6 )(本小题3分。)
6 )(本小题3分。)
(2)已知A=2a2b-ab2,B=-a2b+2ab2。(本小题6分。)
① 求5A+4B;
② 若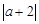 +(3-b)2=0,求5A+4B的值;
+(3-b)2=0,求5A+4B的值;
③试将a2b+ab2用A与B的式子表示出来。
(本题8分,每小题4分。)解方程:
① 4(x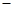 1)=1
1)=1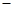 x②
x②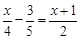
七年级某班为举行游艺活动采购了一批奖品,下面是该班班长与售货员的对话:
班长:阿姨,您好!
售货员:你好,想买点什么?
班长:我这里是100元,请你帮我买10支钢笔和15本笔记本。
售货员:好的,每只钢笔比每本笔记本贵2元,现找你5元,请你收好,再见!
根据这段对话,你能列出一元一次方程求出笔记本和钢笔的单价吗?