在图①至图③中，已知△ABC的面积为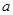
.
（1）如图①，延长△ABC的边BC到点D，使CD=BC，连结DA。若△ACD的面积为S1，则S1=______（用含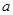的代数式表示）；
（2）如图②，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S2，则S2=__________（用含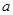的代数式表示）；
（3）在图①—②的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图③）．
阴影部分的面积为S3，则S3=__________（用含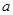的代数式表示），并运用上述（2）的结论写出理由.
理由: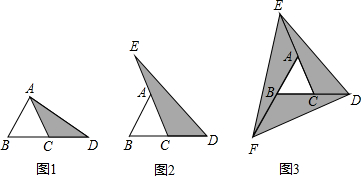
你能化简（
）(
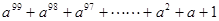)吗？我们不妨先从简单情况入手，现规律，归纳结论.
（1）先填空：（）(
)=；()(
)=； ()(
)=；……
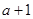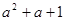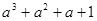由此猜想（）(
)=.
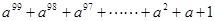（2）利用这个结论，你能解决下面两个问题吗？
①2199＋2198＋2197＋……＋22＋2＋1；
②若
，则
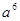等于多少？
如图，△ABC中，AD是BC上的高，AE平分∠BAC，∠B=75°，∠C=45°，求∠DAE与∠AEC的度数.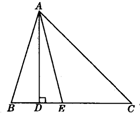
八年级学生周末乘车到游览区游览，游览区距学校120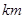
。一部分学生乘慢车先行，出发1
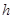后，另一部分学生乘快车前往，结果他们同时到达游览区。已知快车的速度是慢车速度的1.5倍，求慢车的速度.
在图中，画出△ABC关于
轴对称的△A1B1C1，写出△ABC关于
轴对称的△A2B2C2的各点坐标.
为⊙O的弦，
为劣弧
，求
；
，且点
在⊙O的外部，判断
与⊙O的位置关系，并说明理由．