你能化简( )(
)(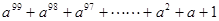 )吗?我们不妨先从简单情况入手,现规律,归纳结论.
)吗?我们不妨先从简单情况入手,现规律,归纳结论.
(1)先填空:( )(
)(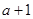 )= ;(
)= ;( )(
)(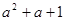 )= ; (
)= ; ( )(
)(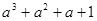 )= ;……
)= ;……
由此猜想( )(
)(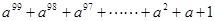 )= .
)= .
(2)利用这个结论,你能解决下面两个问题吗?
①2199+2198+2197+……+22+2+1;
②若 ,则
,则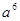 等于多少?
等于多少?
解不等式组: .
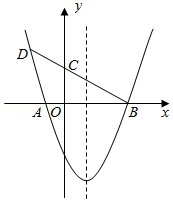
如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , .
(1)求 , 的值;
(2)求直线 的函数解析式;
(3)点 在抛物线的对称轴上且在 轴下方,点 在射线 上.当 与 相似时,请直接写出所有满足条件的点 的坐标.
如图,点 是反比例函数 图象上一点,过点 分别向坐标轴作垂线,垂足为 , .反比例函数 的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .
(1)填空: ;
(2)求 的面积;
(3)求证:四边形 为平行四边形.

某社区拟建 , 两类摊位以搞活"地摊经济",每个 类摊位的占地面积比每个 类摊位的占地面积多2平方米.建 类摊位每平方米的费用为40元,建 类摊位每平方米的费用为30元.用60平方米建 类摊位的个数恰好是用同样面积建 类摊位个数的 .
(1)求每个 , 类摊位占地面积各为多少平方米?
(2)该社区拟建 , 两类摊位共90个,且 类摊位的数量不少于 类摊位数量的3倍.求建造这90个摊位的最大费用.
如图1,在四边形 中, , , 是 的直径, 平分 .
(1)求证:直线 与 相切;
(2)如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.
