2013年是一个让人记忆犹新的年份，雾霾天气持续笼罩我国大部分地区，口罩市场出现热销，某旗舰网店用8000元购进甲、乙两种型号的口罩，销售完后共获利2800元，进价和售价如下表：
| 品名 价格 |
甲型口罩 |
乙型口罩 |
| 进价（元/袋） |
20 |
25 |
| 售价（元/袋） |
26 |
35 |
（1）求该网店购进甲、乙两种型号口罩各多少袋？
（2）该网店第二次以原价购进甲、乙两种型号口罩，购进乙种型号口罩袋数不变，而购进甲种型号口罩袋数是第一次的2倍．甲种口罩按原售价出售，而乙种口罩让利销售．若两种型号的口罩都售完，要使第二次销售活动获利不少于3680元，乙种型号的口罩最低售价为每袋多少元？
( 10分)如图，在平面直角坐标系中，Rt△OAB的直角边OA在x轴的正半轴上，点B在第象限，将△OAB绕点O按逆时针方向旋转至△OA′B′，使点B的对应点B′落在y轴的正半轴上，已知OB=2，
(1)求点B和点A′的坐标；
(2)求经过点B和点B′的直线所对应的一次函数解析式，并判断点A是否在直线BB′上。
已知：如图，四边形
是矩形，
和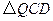
都是等边三角形，且点
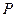在矩形上方，点
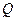在矩形内．
（1） 求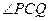
的度数；
（2） 求证：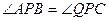
．
（本题11分）如图，已知二次函数的图象经过点A（3，3）、B（4，0）和原点O．
为二次函数图象上的一个动点，过点P作
轴的垂线，垂足为D（m，0），并与直线OA交于点C．
⑴ 求出二次函数的解析式；
⑵ 当点P在直线OA的上方时，求线段PC的最大值．
⑶ 当
时，探索是否存在点，使得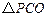
为等腰三角形，如果存在，求出的坐标；如果不存在，请说明理由．
（本题10分）如图，梯形ABCD中，AD∥BC，BC=2AD，F、G分别为边BC、CD的中点，连接AF，FG，过D作DE∥GF交AF于点E。
（1）证明△AED≌△CGF
（2）若梯形ABCD为直角梯形，判断四边形DEFG是什么特殊四边形？并证明你的结论。
 |
（本题10分）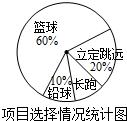
某中学九年级1班同学积极响应“阳光体育工程”的号召，利用课外活动时间积极参加体育锻炼，每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练，训练前后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表．
请你根据图表中的信息回答下列问题：
（1）求选择长跑训练的人数占全班人数的百分比及该班学生的总人数；
（2）求训练后篮球定时定点投篮人均进球数；
（3）根据测试资料，训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%。请求出参加训练之前的人均进球数。