对于集合M,定义函数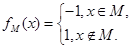 对于两个集合M,N,定义集合
对于两个集合M,N,定义集合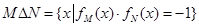 . 已知A={2,4,6,8,10},B={1,2,4,8,16}.
. 已知A={2,4,6,8,10},B={1,2,4,8,16}.
(Ⅰ)写出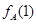 和
和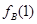 的值,并用列举法写出集合
的值,并用列举法写出集合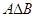 ;
;
(Ⅱ)用Card(M)表示有限集合M所含元素的个数.
(ⅰ)求证:当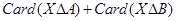 取得最小值时,2∈M;
取得最小值时,2∈M;
(ⅱ)求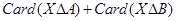 的最小值.
的最小值.
设函数f(x)=Asin(ωx+ )(其中A>0,ω>0,-π<
)(其中A>0,ω>0,-π< ≤π)在x=
≤π)在x= 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 .
.
(1)求f(x)的解析式;
(2)求函数g(x)= 的值域.
的值域.
设函数f(x)=sin2ωx+2 sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1).
,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ,0),求函数f(x)的值域.
,0),求函数f(x)的值域.
已知向量a=(cosx,- ),b=(
),b=( sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b.
(1)求f(x)的最小正周期.
(2)求f(x)在[0, ]上的最大值和最小值.
]上的最大值和最小值.
已知圆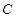 :
:
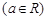 ,过定点
,过定点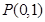 作斜率为1的直线交圆
作斜率为1的直线交圆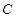 于
于 、
、 两点,
两点,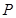 为线段
为线段 的中点.
的中点.
(1)求 的值;
的值;
(2)设 为圆
为圆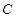 上异于
上异于 、
、 的一点,求△
的一点,求△ 面积的最大值;
面积的最大值;
(3)从圆外一点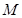 向圆
向圆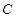 引一条切线,切点为
引一条切线,切点为 ,且有
,且有 , 求
, 求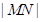 的最小值,并求
的最小值,并求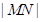 取最小值时点
取最小值时点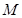 的坐标.
的坐标.
圆 内有一点
内有一点 ,
, 为过点
为过点 且倾斜角为
且倾斜角为 的弦.
的弦.
(1)当 时,求
时,求 ;
;
(2)当弦 被点
被点 平分时,求出直线
平分时,求出直线 的方程;
的方程;
(3)设过 点的弦的中点为
点的弦的中点为 ,求点
,求点 的坐标所满足的关系式.
的坐标所满足的关系式.